题目内容
已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)=f′(x)+6x的图象关于y轴对称.
(1)求m,n的值及函数y=f(x)的单调区间;
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解析:(1)由函数f(x)的图象过点(-1,-6),得m-n=-3.①
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n.
而g(x)的图象关于y轴对称,所以m=-3.代入①得n=0.
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>0得x>2或x<0,由f′(x)<0,得0<x<2,
∴f(x)的单调递增区间是(-∞,0)和(2,+∞);f(x)的单调递减区间是(0,2).(注:用∪扣2分)
(2)由(1)得
①当0<a<1时,f(x)在(a-1,a+1)内有极大值f(0)=-2,无极小值;
②当a=1时,f(x)在(a-1,a+1)内无极值;
③当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
④当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得,当0<a<1时,f(x)有极大值-2,无极小值;
当1<a<3时,f(x)有极小值-6,无极大值;
当a=1或a≥3时,f(x)无极值.

练习册系列答案
相关题目
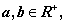 则
则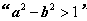 是
是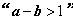 的 ( )
的 ( )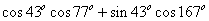 = .
= .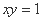 ,直线
,直线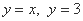 所围成的平面图形的面积为 ( )
所围成的平面图形的面积为 ( )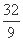 B.
B.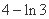 C.
C.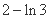 D.
D.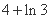
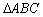 中,若
中,若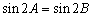 ,则
,则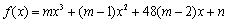 在区间
在区间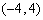 上是单调减函数.
上是单调减函数.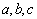 满足
满足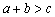 ,则
,则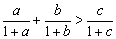 ;
; +cos
+cos  ,若(z1-z2)2+(z2-z3)2=0 则z1=z2=z3;
,若(z1-z2)2+(z2-z3)2=0 则z1=z2=z3; 的离心率为2,则
的离心率为2,则
 C.
C.  D. 1
D. 1 ,
, 满足约束条件
满足约束条件 且
且 的最小值为7,则
的最小值为7,则 是双曲线
是双曲线 :
: 的一个焦点,则点
的一个焦点,则点 .
.
 .3
.3 
 .
.
 ”的否定是( )
”的否定是( ) B.
B. 
 D.
D. 