题目内容
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,DE=2AB=2,且F是CD的中点.
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE;
(Ⅲ)设AC=2m,当m为何值时?使得平面BCE与平面ACD所成的二面角的大小为45°.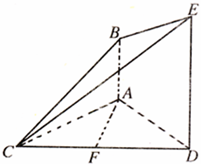
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE;
(Ⅲ)设AC=2m,当m为何值时?使得平面BCE与平面ACD所成的二面角的大小为45°.

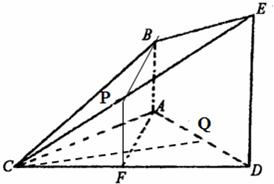
(I)取CE中点P,连接FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP=
| 1 |
| 2 |
又AB∥DE,且AB=
| 1 |
| 2 |
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,
∴AF∥BP.
又∵AF?平面BCE,BP?平面BCE,
∴AF∥平面BCE.
(II)∵△ACD为正三角形,
∴AF⊥CD.
∵AB⊥平面ACD,DE∥AB,
∴DE⊥平面ACD,又AF?平面ACD,
∴DE⊥AF又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE.
又BP∥AF,∴BP⊥平面CDE.
又∵BP?平面BCE,
∴平面BCE⊥平面CDE.
(Ⅲ) 由题意可知,△CBE中,CB=EB=
| 1+4m2 |
| 1+m2 |
∴S△CBE=m
| 3(1+m2) |
∵平面BCE与平面ACD所成的二面角的大小为45°
∴cos45°=
| ||
m
|
| ||
| 2 |
∴m=1

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.