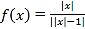题目内容
【题目】已知点![]() .若曲线
.若曲线![]() 上存在
上存在![]() ,
,![]() 两点,使
两点,使![]() 为正三角形,则称
为正三角形,则称![]() 为
为![]() 型曲线.给定下列三条曲线:
型曲线.给定下列三条曲线:
①![]() ;
;
②![]() ;
;
③![]() .
.
其中![]() 型曲线的个数是
型曲线的个数是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
对于①,A(-1,1)到直线y=-x+3的距离为![]() ,若直线上存在两点B,C,使△ABC为正三角形,则|AB|=|AC|=
,若直线上存在两点B,C,使△ABC为正三角形,则|AB|=|AC|=![]() ,以A为圆心,以
,以A为圆心,以![]() 为半径的圆的方程为(x+1)2+(y-1)2=6,联立
为半径的圆的方程为(x+1)2+(y-1)2=6,联立![]()
解得![]() ,或
,或![]() ,后者小于0,所以对应的点不在曲线上,所以①不是.
,后者小于0,所以对应的点不在曲线上,所以①不是.
对于②,![]() 化为
化为![]() ,图形是第二象限内的四分之一圆弧,此时连接A点与圆弧和两坐标轴交点构成的三角形顶角最小为135°,所以②不是.
,图形是第二象限内的四分之一圆弧,此时连接A点与圆弧和两坐标轴交点构成的三角形顶角最小为135°,所以②不是.
对于③,根据对称性,若![]() 上存在两点B、C使ABC构成正三角形,则两点连线的斜率为1,设BC所在直线方程为x-y+m=0,由题意知A到直线距离为直线被
上存在两点B、C使ABC构成正三角形,则两点连线的斜率为1,设BC所在直线方程为x-y+m=0,由题意知A到直线距离为直线被![]() 所截弦长的
所截弦长的![]() 倍,列方程解得m=-
倍,列方程解得m=-![]() ,所以曲线③是T型线.
,所以曲线③是T型线.

练习册系列答案
相关题目
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点
元/分计费.已知王先生家离上班地点![]() 公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间 ![]() (分)是一个随机变量.现统计了
(分)是一个随机变量.现统计了![]() 次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 |
|
|
|
|
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.(1)写出王先生一次租车费用
分.(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;(2)若王先生一次开车时间不超过
(分)的函数关系式;(2)若王先生一次开车时间不超过![]() 分为“路段畅通”,设
分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.