Question

若对任意满足的实数x、y，不等式axy≥x²+y²恒成立，则实数a的取值范围是________．

Answer 1

分析：不等式组，表示一个三角形区域，三角形的三个顶点的坐标分别为（1，4），（3，6），（3，2）
与原点连线的斜率分别为4，2，，可求的，不等式axy≥x²+y²可转化为，求出右边的最小值，即可求得实数a的取值范围．
解答：不等式组，表示一个三角形区域，三角形的三个顶点的坐标分别为（1，4），（3，6），（3，2）
与原点连线的斜率分别为4，2，
∴
不等式axy≥x²+y²可转化为
令，则在上单调减，在[1，4]上单调增
∴t=1时，函数取得最小值为2；t=4时，函数取得最大值为
∴
故答案为：
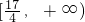
点评：本题考查恒成立问题，考查函数的单调性与最值，解题的关键是分离参数，确定函数的最值．