题目内容
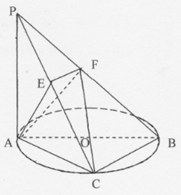
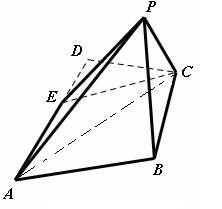
如图, 平面
平面 ,
, ,
,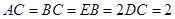 ,
, ,
, 分别为
分别为 的中点.
的中点.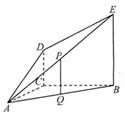
(I)证明: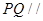 平面
平面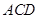 ;
;
(II)求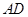 与平面
与平面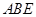 所成角的正弦值.
所成角的正弦值.
(I)只需证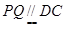 ;(II)
;(II)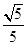 。
。
解析试题分析:(I)证明:连接 , 在
, 在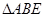 中,
中, 分别是
分别是 的中点,所以
的中点,所以 , 又
, 又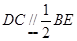 ,所以
,所以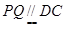 ,又
,又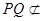 平面ACD ,DC
平面ACD ,DC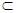 平面ACD, 所以
平面ACD, 所以 平面ACD。
平面ACD。
(Ⅱ)在 中,
中,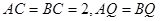 ,所以
,所以
而DC 平面ABC,
平面ABC,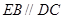 ,所以
,所以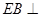 平面ABC
平面ABC
而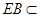 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE 平面ABC, 所以
平面ABC, 所以 平面ABE
平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以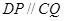
所以 平面ABE, 所以直线AD在平面ABE内的射影是AP,
平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是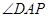
在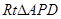 中,
中, ,
,
所以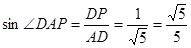 。
。
考点:线面平行的判定定理;线面角。
点评:本题主要考查了空间中直线与平面所成的角,属立体几何中的常考题型,较难.本题也可以用向量法来做。而对于利用向量法求线面角关键是正确写出点的坐标和求解平面的一个法向量。注意计算要仔细、认真。

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 ⊙
⊙ 所在的平面,
所在的平面,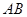 是⊙
是⊙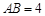 ,C是⊙
,C是⊙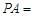
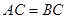 ,
,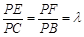 .
.
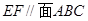 ;
;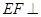
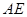 ;
;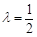 时,求三棱锥
时,求三棱锥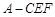 的体积.
的体积.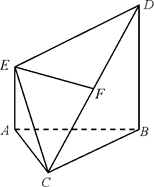
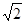 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.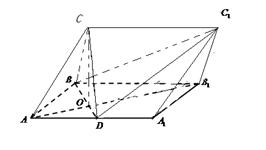
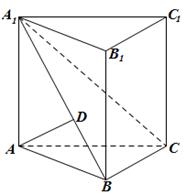
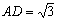 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥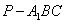 的体积。
的体积。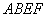 所在平面与直角梯形
所在平面与直角梯形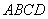 所在平面互相垂直,
所在平面互相垂直,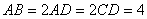 ,
,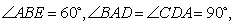 点
点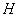 ,
,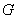 分别是线段
分别是线段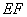 ,
, 的中点.
的中点. 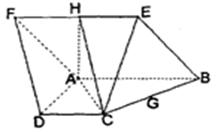
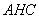
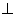 平面
平面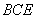 ;
;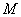 在直线
在直线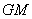 //平面
//平面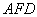 ,求平面
,求平面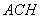 与平面
与平面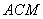 所成角的余弦值。
所成角的余弦值。 .
.
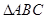 中,
中, 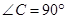 ,
,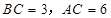 .D、E分别是
.D、E分别是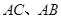 上的点,且
上的点,且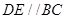 .将
.将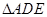 沿
沿 折起到
折起到 的位置,使
的位置,使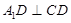 ,如图2.
,如图2.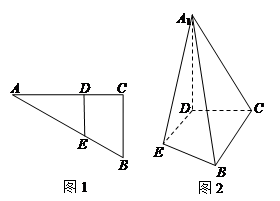
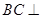 平面
平面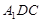 ;
;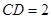 ,求
,求 与平面
与平面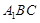 所成角的正弦值;
所成角的正弦值;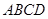 中,
中,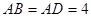 ,
,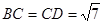 ,点
,点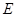 为线段
为线段 上的一点.现将
上的一点.现将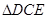 沿线段
沿线段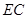 翻折到
翻折到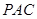 (点
(点 与点
与点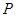 重合),使得平面
重合),使得平面 平面
平面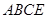 ,连接
,连接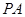 ,
,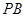 .
.
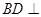 平面
平面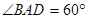 ,且点
,且点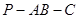 的大小.
的大小.