题目内容
若函数y=f（x）的定义域是[0，2]，则函数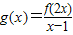
的定义域是（ ）A．[0，1]
B．[0，1）
C．[0，1）∪（1，4]
D．（0，1）
【答案】分析：根据f（2x）中的2x和f（x）中的x的取值范围一样得到：0≤2x≤2，又分式中分母不能是0，即：x-1≠0，解出x的取值范围，得到答案．
解答：解：因为f（x）的定义域为[0，2]，所以对g（x），0≤2x≤2且x≠1，故x∈[0，1），
故选B．
点评：本题考查求复合函数的定义域问题．
解答：解：因为f（x）的定义域为[0，2]，所以对g（x），0≤2x≤2且x≠1，故x∈[0，1），
故选B．
点评：本题考查求复合函数的定义域问题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目