题目内容
若函数f(x)=sinax+cosax(a>0)的最小正周期为1,则它的图象的一个对称中心为( )
A.(-
| B.(0,0) | C.(-
| D.(
|
f(x)=sinax+cosax=
sin(ax+
)
T=
=1,则a=2π
所以f(x)=
sin(2πx+
)
令f(x)=0,则其中有:2πx+
=0
x=-
即其中一个对称中心是(-
,0)
故选C.
| 2 |
| π |
| 4 |
T=
| 2π |
| a |
所以f(x)=
| 2 |
| π |
| 4 |
令f(x)=0,则其中有:2πx+
| π |
| 4 |
x=-
| 1 |
| 8 |
即其中一个对称中心是(-
| 1 |
| 8 |
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有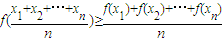 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题: ;
; .
.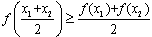 ,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有 (当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题: ,则
,则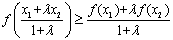 ;
; .
.