题目内容
已知函数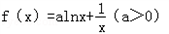 .
.
(I)求函数f(x)的单调区间和极值;
(II)若 x>0,均有ax(2﹣lnx)≤1,求实数a的取值范围.
x>0,均有ax(2﹣lnx)≤1,求实数a的取值范围.
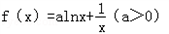 .
.(I)求函数f(x)的单调区间和极值;
(II)若
 x>0,均有ax(2﹣lnx)≤1,求实数a的取值范围.
x>0,均有ax(2﹣lnx)≤1,求实数a的取值范围.解:(I)依题意,x>0,f′(x)=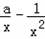
由f′(x)>0得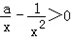 ,
,
解得x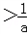 ,
,
函数f(x)的单调增区间为( ,+∞)
,+∞)
由f′(x)<0得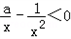 ,
,
解得x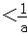 ,
,
函数f(x)的单调减区间为(0, )
)
∴当x= 时,函数f(x)的极小值为f(
时,函数f(x)的极小值为f( )=aln
)=aln +a=a﹣alna
+a=a﹣alna
(II)设g(x)=ax(2﹣lnx)=2ax﹣axlnx,
则函数定义域为(0,+∞)
g′(x)=2a﹣(ax +alnx)=a(1﹣lnx)
+alnx)=a(1﹣lnx)
由g′(x)=0,解得x=e,
由a>0可知,
当x∈(0,e)时,g′(x)>0,函数g(x)单调递增,
当x∈(e,+∞)时,g′(x)<0,函数g(x)单调递减,
∴函数g(x)的最大值为g(e)=ae(2﹣lne)=ae
要使不等式恒成立,只需g(x)的最大值不大于1即可,
即g(e)≤1也即ae≤1,解得 a≤
又∵a>0
∴0<a≤
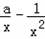
由f′(x)>0得
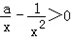 ,
,解得x
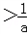 ,
,函数f(x)的单调增区间为(
 ,+∞)
,+∞)由f′(x)<0得
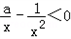 ,
,解得x
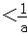 ,
,函数f(x)的单调减区间为(0,
 )
)∴当x=
 时,函数f(x)的极小值为f(
时,函数f(x)的极小值为f( )=aln
)=aln +a=a﹣alna
+a=a﹣alna(II)设g(x)=ax(2﹣lnx)=2ax﹣axlnx,
则函数定义域为(0,+∞)
g′(x)=2a﹣(ax
 +alnx)=a(1﹣lnx)
+alnx)=a(1﹣lnx)由g′(x)=0,解得x=e,
由a>0可知,
当x∈(0,e)时,g′(x)>0,函数g(x)单调递增,
当x∈(e,+∞)时,g′(x)<0,函数g(x)单调递减,
∴函数g(x)的最大值为g(e)=ae(2﹣lne)=ae
要使不等式恒成立,只需g(x)的最大值不大于1即可,
即g(e)≤1也即ae≤1,解得 a≤

又∵a>0
∴0<a≤


练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.