题目内容
函数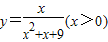 的最大值是 .
的最大值是 .
【答案】分析:原函数分子分母同除以x可化为y=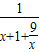 ,令分母为u,可由基本不等式求u的最小值,即可得原函数的最大值.
,令分母为u,可由基本不等式求u的最小值,即可得原函数的最大值.
解答:解:∵x>0,∴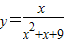 =
=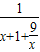
令u=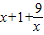 ,(x>0)由基本不等式可得:
,(x>0)由基本不等式可得:
u=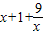 =1
=1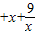
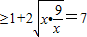 ,
,
当且仅当x=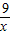 ,即x=3时取到等号,故u的最小值为7,
,即x=3时取到等号,故u的最小值为7,
故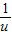 的最大值为
的最大值为 ,即函数
,即函数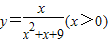 的最大值为:
的最大值为:
故答案为:
点评:本题为基本不等式求最值,原函数分子分母同除以x转化为基本不等式是解决问题的关键,属基础题.
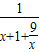 ,令分母为u,可由基本不等式求u的最小值,即可得原函数的最大值.
,令分母为u,可由基本不等式求u的最小值,即可得原函数的最大值.解答:解:∵x>0,∴
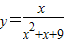 =
=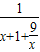
令u=
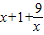 ,(x>0)由基本不等式可得:
,(x>0)由基本不等式可得:u=
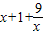 =1
=1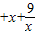
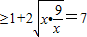 ,
,当且仅当x=
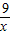 ,即x=3时取到等号,故u的最小值为7,
,即x=3时取到等号,故u的最小值为7,故
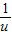 的最大值为
的最大值为 ,即函数
,即函数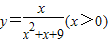 的最大值为:
的最大值为:
故答案为:

点评:本题为基本不等式求最值,原函数分子分母同除以x转化为基本不等式是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知二次函数y=ax2+(a2+1)x在x=1处的导数值为1,则该函数的最大值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|