题目内容
已知函数f(x)=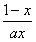 +lnx,
+lnx,
(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求正实数a的取值范围;
(Ⅱ)若a=1,k∈R且k<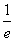 ,设F(x)=f(x)+(k-1)lnx,求函数F(x)在[
,设F(x)=f(x)+(k-1)lnx,求函数F(x)在[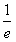 ,e]上的最大值和最小值。
,e]上的最大值和最小值。
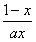 +lnx,
+lnx,(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求正实数a的取值范围;
(Ⅱ)若a=1,k∈R且k<
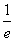 ,设F(x)=f(x)+(k-1)lnx,求函数F(x)在[
,设F(x)=f(x)+(k-1)lnx,求函数F(x)在[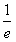 ,e]上的最大值和最小值。
,e]上的最大值和最小值。 解:(Ⅰ)由题设可得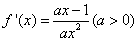 ,
,
因为函数f(x)在[1,+∞)上是增函数,
所以,当x∈[1,+∞)时,不等式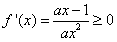 即
即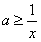 恒成立,
恒成立,
因为,当x∈[1,+∞)时,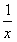 的最大值为1,
的最大值为1,
则实数a的取值范围是[1,+∞)。
(Ⅱ)a=1,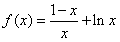 ,
,
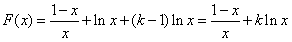 ,
,
所以,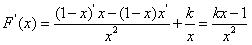 ,
,
(1)若k=0,则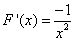 ,在
,在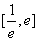 上,恒有F′(x)<0,
上,恒有F′(x)<0,
所以F(x)在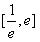 上单调递减,
上单调递减,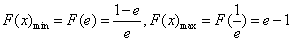 ;
;
(2)k≠0时,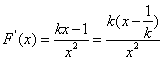 ,
,
i)若k<0,在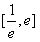 上,恒有
上,恒有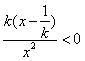 ,所以F(x)在
,所以F(x)在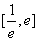 上单调递减,
上单调递减,
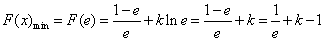 ,
,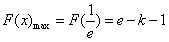 ;
;
ii)k>0时,因为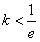 ,所以
,所以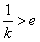 ,
,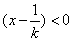 ,
,
所以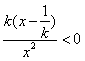 ,所以F(x)在
,所以F(x)在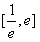 上单调递减,
上单调递减,
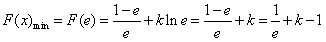 ,
,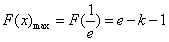 ;
;
综上所述:当k=0时,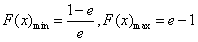 ;
;
当k≠0 且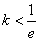 时,
时,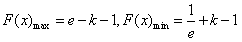 。
。
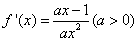 ,
,因为函数f(x)在[1,+∞)上是增函数,
所以,当x∈[1,+∞)时,不等式
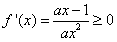 即
即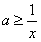 恒成立,
恒成立,因为,当x∈[1,+∞)时,
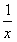 的最大值为1,
的最大值为1,则实数a的取值范围是[1,+∞)。
(Ⅱ)a=1,
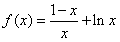 ,
,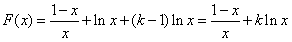 ,
,所以,
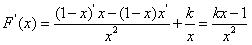 ,
,(1)若k=0,则
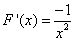 ,在
,在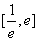 上,恒有F′(x)<0,
上,恒有F′(x)<0,所以F(x)在
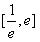 上单调递减,
上单调递减,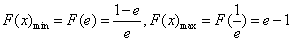 ;
;(2)k≠0时,
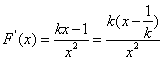 ,
,i)若k<0,在
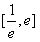 上,恒有
上,恒有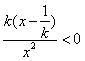 ,所以F(x)在
,所以F(x)在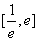 上单调递减,
上单调递减,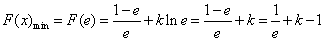 ,
,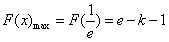 ;
;ii)k>0时,因为
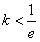 ,所以
,所以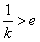 ,
,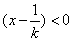 ,
,所以
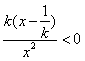 ,所以F(x)在
,所以F(x)在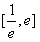 上单调递减,
上单调递减,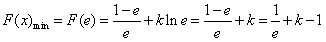 ,
,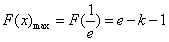 ;
;综上所述:当k=0时,
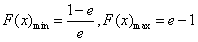 ;
;当k≠0 且
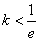 时,
时,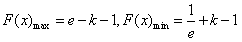 。
。
练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|