题目内容
| |
：
的焦点为
，椭圆
：
的离心率
，与在第一象限的交点为P
. (1)求抛物线及椭圆的方程；
(2)已知直线
：
与椭圆交于不同
两点
，
，点
满足
，直线
的斜率为
，试证明
.
解：（1）∵为与在第一象限的交点 ∴
……1分
∴抛物线的方程为
……2分
∵椭圆的离心率
……3分
∴
……4分
又∵为与在第一象限的交点
∴
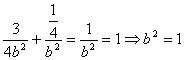
……5分
∴椭圆的方程
……6分
（2）把代入得，
……7分
……8分
设
，
，则
，
……9分
∵∴为
的中点 ∴
，
∴点的坐标为
……10分
∵
∴
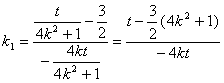……11分
∴
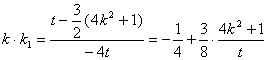……12分
∵
∴
∴……14分
练习册系列答案
互动英语系列答案
相关题目
如图，抛物线S的顶点在原点O，焦点在x轴上，△ABC三个顶点都在抛物线上，且△ABC的重心为抛物线的焦点，若BC所在直线方程为4x+y-20=0，（本小题满分13分）
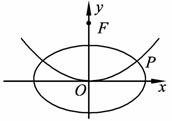
如图，椭圆C: 
的焦点为F1（0，c）、F2（0，一c）（c>0），抛物线
的焦点与F1重合，过F2的直线l与抛物线P相切，切点在第一象限，且与椭圆C相交于A、B两点，且
（I）求证：切线l的斜率为定值
|
22．（本题满分15分）已知抛物线C的顶点在原点,焦点在y轴正半轴上,点
到其准线的距离等于5．
（Ⅰ）求抛物线C的方程;
（Ⅱ）如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆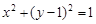
交于A、C、D、B四点,试证明
为定值;
|
且交于点M,求
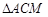与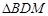
面积之和的最小值．
到其准线的距离等于5．
交于A、C、D、B四点,试证明
为定值;
且
与
面积之和的最小值．