题目内容
(本题满分14分)已知圆 和圆外一点
和圆外一点 .
.
(1)过 作圆的割线交圆于
作圆的割线交圆于 两点,若|
两点,若|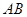 |=4,求直线
|=4,求直线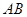 的方程;
的方程;
(2)过 作圆的切线,切点为
作圆的切线,切点为 ,求切线长及
,求切线长及 所在直线的方程.
所在直线的方程.
【答案】
(1)直线 的方程
的方程 或
或 (2)切线长为
(2)切线长为
 所在直线的方程为
所在直线的方程为
【解析】
试题分析:(1)圆的方程可化为: ,圆心为
,圆心为 ,半径
,半径
①若割线斜率存在,设 :
: ,即
,即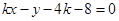 ,
,
设 的中点为
的中点为 ,则|PN|=
,则|PN|=
由 得
得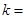
 则直线
则直线 :
: . ……4分
. ……4分
②若割线斜率不存在,则直线 :
: ,代入圆方程得
,代入圆方程得 ,
,
解得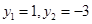 符合题意,
符合题意,
综上,直线 的方程为
的方程为 或
或 .
……7分
.
……7分
(2)切线长为
以 为直径的圆的方程为
为直径的圆的方程为 ,
,
即 .
.
又已知圆的方程为 ,两式相减,得
,两式相减,得 ,
,
所以直线 的方程为
的方程为 .
……14分
.
……14分
考点:本小题主要考查直线与圆的位置关系、圆与圆的位置关系以及弦长公式的应用,考查学生综合运用知识解决问题的能力和运算求解能力.
点评:要解决好此类问题就要牢固掌握直线与圆的位置关系的判断,注重圆的几何性质在解题的中的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
