题目内容
下列命题中正确的是
- A.若a>b,则am2>bm2
- B.若

- C.若

- D.若

C
分析:若 m2=0,可得A不正确.若c<0,则由a>b,推出 ,故 B 不正确.利用不等式性质可得
,故 B 不正确.利用不等式性质可得
C 正确. 令 a=-2,b=-1,可得 D 不正确.
解答:若 m2=0,则由a>b,推出 am2=bm2,故A不正确.
若c<0,则由a>b,推出 ,故 B 不正确.
,故 B 不正确.
若 a>b,ab>0 则可得到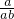 >
>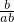 ,即
,即  ,故 C 正确.
,故 C 正确.
若 a2>b2,ab>0,令 a=-2,b=-1,可得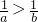 ,故D 不正确.
,故D 不正确.
故选 C.
点评:本题考查不等式与不等关系,不等式性质的应用,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.
分析:若 m2=0,可得A不正确.若c<0,则由a>b,推出
 ,故 B 不正确.利用不等式性质可得
,故 B 不正确.利用不等式性质可得C 正确. 令 a=-2,b=-1,可得 D 不正确.
解答:若 m2=0,则由a>b,推出 am2=bm2,故A不正确.
若c<0,则由a>b,推出
 ,故 B 不正确.
,故 B 不正确.若 a>b,ab>0 则可得到
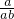 >
>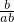 ,即
,即  ,故 C 正确.
,故 C 正确.若 a2>b2,ab>0,令 a=-2,b=-1,可得
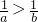 ,故D 不正确.
,故D 不正确.故选 C.
点评:本题考查不等式与不等关系,不等式性质的应用,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,
, 及平面
及平面 ,
, ,下列命题中正确的是
,下列命题中正确的是 ,
, ,则
,则 ;
;  ,则
,则 ,
, ,则
,则 ;
;
 ,则
,则 .
. 唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).
唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).  则下列命题中正确的是
则下列命题中正确的是 的最小正周期为
的最小正周期为
 的最小值为
的最小值为
