Question

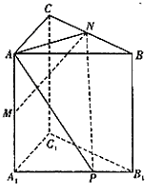在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AC=BC=1，侧棱AA₁=

2

，M，N分别为棱AA₁、BC的中点，点P在边A₁B₁上，且A₁P=2PB₁．
（1）求证：MN⊥AP；
（2）求二面角M-AN-P的正切值．

Answer 1

分析：（1）过点N作NH⊥AB于H，连接MN．由题意可得：NH⊥面ABB₁A₁，所以MH为MN在面ABB₁A₁内的射影，且AH=

3

4

2

，再结合解三角形的知识即可得到答案．  
（2）根据线面关系作出二面角的平面角，再证明此是二面角的平面角，然后放入三角形中利用解三角形的有关知识夹角问题即可．

解答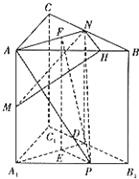：解：（1）证明：过点N作NH⊥AB于H，连接MN．
∵ABC-A₁B₁C₁为直三棱柱，且NH⊥AB，
∴NH⊥面ABB₁A₁，
∴MH为MN在面ABB₁A₁内的射影，且AH=

3

4

2

在Rt△MAH中，tan∠AMH=

AH

AM

=

3

2

，
在Rt△AA₁P中，tan∠APA₁=

AA1

A1P

=

3

2

，
∴∠AMH=∠APA₁，
∵∠A₁AP+∠AMH=∠A₁AP+∠APA₁=90°，
∴MH⊥AP．
由三垂线定理知MN⊥AP．  
（2）取B₁C₁的中点D，连接DN、DA₁
过点P作PF⊥AD于E，过E作EF⊥AN于F，连接PF，
由三垂线定理知：∠PFE为二面角M-AN-P的平面角．
在△A₁B₁D中，cos∠B₁A₁D=

A1 B 2 1 +A1D2-B1D2

2A1B1•A1D

=

3 10

10

，
在Rt△PEA₁中，PE=A₁P•sin∠B₁A₁D=

2 5

15

，
∴tan∠PFE=

PE

EF

=

2 5 15

2

=

10

15

．
故二面角M-AN-P的正切值为

10

15

．

点评：解决此类问题的关键是熟练掌握几何体的结构特征，根据其特征得到线面的位置关系，进而解决平行关系与垂直关系以及空间角等问题．