题目内容
在数列{an }中,已知a1=1,a2=5,an+2=an+1-an (n∈N※),则a2006 等于( )
分析:先根据数列的递推公式求出数列的前几项,根据项的特点,发现数列的周期性规律,从而可求
解答:解:∵a1=1,a2=5,an+2=an+1-an,
∴a3=4,a4=-1,a5=-5,a6=-4,a7=1=a1
数列{an }是以6为周期的数列
∴a2006=a2=5
故选D
∴a3=4,a4=-1,a5=-5,a6=-4,a7=1=a1
数列{an }是以6为周期的数列
∴a2006=a2=5
故选D
点评:本题主要考查了利用数列的递推关系求解数列的项,求解的关键是数列的项周期性规律的发现

练习册系列答案
相关题目
 ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*).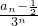 }是等差数列;
}是等差数列; ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*).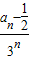 }是等差数列;
}是等差数列;