题目内容
【题目】已知数列{an}的首项a1＝a，Sn是数列{an}的前n项和，且满足： 
＝3n2an＋
，an≠0，n≥2，n∈N*．
(1)若数列{an}是等差数列，求a的值；
(2)确定a的取值集合M，使a∈M时，数列{an}是递增数列．
【答案】（1）3（2）
【解析】试题分析：（1）数列{an}是等差数列，故可从特殊情形出发：先求出a2＝12－2a，a3＝3＋2a．再利用a1＋a3＝2a2，解得a＝3．最后验证.（2）先由通项与和项关系，将已知条件转化为递推关系：an＋1＋an＝6n＋3，(n≥2)．an＋2－an＝6，(n≥2)，即数列a2，a4，a6， ，及数列a3，a5，a7， 都是公差为6的等差数列，要使数列{an}是递增数列，须有a1＜a2
，解得
＜a＜
．
试题解析：（1）在
＝3n2an＋
中分别令n＝2，n＝3，及a1＝a得
(a＋a2)2＝12a2＋a2，(a＋a2＋a3)2＝27a3＋(a＋a2)2，
因an≠0，所以a2＝12－2a，a3＝3＋2a． 2分
因数列{an}是等差数列，所以a1＋a3＝2a2，即2(12－2a)＝a＋3＋2a，解得a＝3． 4分
经检验a＝3时，an＝3n，Sn＝
，Sn－1＝
满足
＝3n2an＋
（2）由
＝3n2an＋
，得
－
＝3n2an，即(Sn＋Sn－1)(Sn－Sn－1)＝3n2an，
即(Sn＋Sn－1)an＝3n2an，因为an≠0，所以Sn＋Sn－1＝3n2，(n≥2)，① 6分
所以Sn＋1＋Sn＝3(n＋1)2，②
②－①，得an＋1＋an＝6n＋3，(n≥2)．③ 8分
所以an＋2＋an＋1＝6n＋9，④
④－③，得an＋2－an＝6，(n≥2)
即数列a2，a4，a6， ，及数列a3，a5，a7， 都是公差为6的等差数列， 10分
因为a2＝12－2a，a3＝3＋2a．
所以an＝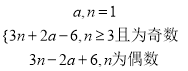
12分
要使数列{an}是递增数列，须有
a1＜a2，且当n为大于或等于3的奇数时，an＜an＋1，且当n为偶数时，an＜an＋1，
即a＜12－2a，
3n＋2a－6＜3(n＋1)－2a＋6(n为大于或等于3的奇数)，
3n－2a＋6＜3(n＋1)＋2a－6(n为偶数)，
解得
＜a＜
．所以M＝
，当a∈M时，数列{an}是递增数列． 16分
