题目内容
已知 (-1<x<1)
(-1<x<1)
(1)判断函数f(x)的奇偶性,并加以证明;
(2)若a,b∈(-1,1),证明: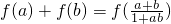 ;
;
(3)证明对任意常数k∈R,f(x)=k有且仅有一解.
解:(1)
又x∈(-1,1),所以函数f(x)是奇函数
(2)若a、b∈(-1,1),f(a)+f(b)=lg +lg
+lg  =lg
=lg 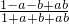 ,
,
f(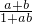 )=lg
)=lg 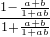 =lg
=lg 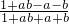 ,∴f(a)+f(b)=f(
,∴f(a)+f(b)=f( 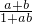 ).
).
(3)设-1<x<1,△x=x2-x1>0,
因为1-x1>1-x2>0;1+x2>1+x1>0所以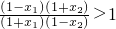
所以 所以函数
所以函数 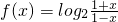 在(-1,1)上是增函数.
在(-1,1)上是增函数.
从而对任意常数k∈R,f(x)=k有且仅有一解.
分析:(1)先求定义域,看是否关于原点对称,再用定义判断.
(2)若a、b∈(-1,1),先化简f(a)+f(b),再化简f(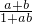 )的解析式,然后作比较发现是相等的式子.
)的解析式,然后作比较发现是相等的式子.
(2)用单调性定义证明,先在定义域上任取两个变量,且界定大小,再作差变形,与0比较.
点评:本题主要考查函数奇偶性和单调性,证明奇偶性一般用定义,证明单调性可用定义或导数法.

又x∈(-1,1),所以函数f(x)是奇函数
(2)若a、b∈(-1,1),f(a)+f(b)=lg
 +lg
+lg  =lg
=lg 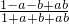 ,
,f(
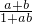 )=lg
)=lg 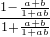 =lg
=lg 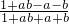 ,∴f(a)+f(b)=f(
,∴f(a)+f(b)=f( 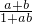 ).
).(3)设-1<x<1,△x=x2-x1>0,

因为1-x1>1-x2>0;1+x2>1+x1>0所以
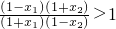
所以
 所以函数
所以函数 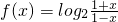 在(-1,1)上是增函数.
在(-1,1)上是增函数.从而对任意常数k∈R,f(x)=k有且仅有一解.
分析:(1)先求定义域,看是否关于原点对称,再用定义判断.
(2)若a、b∈(-1,1),先化简f(a)+f(b),再化简f(
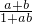 )的解析式,然后作比较发现是相等的式子.
)的解析式,然后作比较发现是相等的式子.(2)用单调性定义证明,先在定义域上任取两个变量,且界定大小,再作差变形,与0比较.
点评:本题主要考查函数奇偶性和单调性,证明奇偶性一般用定义,证明单调性可用定义或导数法.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个. ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式; .…………………………………………4分
.…………………………………………4分 (n∈N*),bn=
(n∈N*),bn= =
= =
= =
= ,
, -1=
-1= n-1=
n-1= =1-an=1-
=1-an=1- =
= ,
,  +
+ +…+
+…+ +
+ +…+
+…+
 =1-
=1- 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表.f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示.若实数a满足f(2a+1)<1,则a的取值范围是
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表.f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示.若实数a满足f(2a+1)<1,则a的取值范围是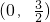



 是增函数,且h(x)的导函数h'(x)存在正零点,求m的值.
是增函数,且h(x)的导函数h'(x)存在正零点,求m的值.