题目内容
矩形ABCD中,AB= 4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )
A. | B. | C. | D.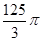 |
A
解析试题分析:因为球心到球面各点的距离相等,即可知道外接球的半径,就可以求出其体积了.
由题意知,球心到四个顶点的距离相等,所以球心在对角线AC上,且其半径为AC长度的一半,则V球= ,故选A.
,故选A.
考点:本试题主要考查了学生的思维意识,对球的结构和性质的运用,是基础题
点评:解决该试题的关键是理解对折后的图形中球心的位置,同时要利用直二面角得到各边长,分析一个三角形的外接圆的圆心是突破口,进而得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法不正确的是( )
| A.空间中,一组对边平行且相等的四边形是一定是平行四边形; |
| B.过一条直线有且只有一个平面与已知平面垂直. |
| C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内; |
D.存在两条异面直线 ,使得 ,使得 ; ; |
已知一个球的内接正方体棱长为1,则这个球的表面积为( )
A. | B. | C. | D. |
 的所有顶点都在球O的表面上,三角形ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )
的所有顶点都在球O的表面上,三角形ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )



 ),则该棱锥的体积是( )
),则该棱锥的体积是( )




 分别是正方体的棱的中点,那么,在原正方体中,
分别是正方体的棱的中点,那么,在原正方体中, 与
与 所在直线为异面直线的是
所在直线为异面直线的是