题目内容

在△ABC中，三个内角满足条件A+C=2B，它的面积为10，周长为20，求三角形的三边长.

思路分析：由条件A+C=2B，可求出其中一个内角，再根据已知的周长和面积，可列出三边所满足的两个方程.结合余弦定理，利用上面列出的关系即可求解.

解：设角A，B，C所对的边分别为a、b、c.

由A+C=2B及A+B+C=π,可得

B=,A+C=.

由已知条件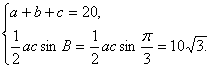,可得整理,可得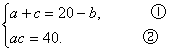

再由余弦定理有

b2=a2+c2-2accosB

=a2+c2-2accos

=(a+c)2-3ac

=(20-b)2-120,

所以b2=400-40b+b2-120.所以b=7.

代入①得解得或

所以三角形的三边分别为5，7，8.

方法归纳 已知边长的和与积的表达式，常结合运用余弦定理的变形：

b2=a2+c2-2accosB=(c+a)2-2ca(1+cosB).

练习册系列答案
相关题目
8、对于直角坐标平面内的任意两点A（x1，y1），B（x2，y2），定义它们之间的一种“距离”：||AB||=|x2-x1|+|y2-y1|．给出下列三个命题：
①若点C在线段AB上，则||AC||+||CB||=||AB||；
②在△ABC中，若∠C=90o，则||AC||2+||CB||2=||AB||2；
③在△ABC中，||AC||+||CB||＞||AB||．
其中真命题的个数为（　　）
△ABC中，三个内角A、B、C所对的边分别为a、b、c，设复数z=sinA（sinA-sinC）+（sin2B-sin2C）i，且z在复平面内所对应的点在直线y=x上．
（1）求角B的大小；
（2）若sinB=cosAsinC，△ABC的外接圆的面积为4π，求△ABC的面积．
对于直角坐标平面内的任意两点A（x1，y1）、B（x2，y2），定义它们之间的一种“距离”：‖AB‖=|x1-x2|+|y1-y2|．给出下列三个命题：
①若点C在线段AB上，则‖AC‖+‖CB‖=‖AB‖；
②在△ABC中，若∠C=90°，则‖AC‖+‖CB‖=‖AB‖；
③在△ABC中，‖AC‖+‖CB‖＞‖AB‖．
其中真命题的个数为（　　）
①“若x+y=0，则x，y互为相反数”的逆命题是“若x，y互为相反数，则x+y=0”．
②在平面内，F1、F2是定点，|F1F2|=6，动点M满足||MF1|-|MF2||=4，则点M的轨迹是双曲线．
③“在△ABC中，“∠B=60°”是“∠A，∠B，∠C三个角成等差数列”的充要条件．
④“若-3＜m＜5则方程
x2
5-m
+
y2
m+3
=1是椭圆”．
⑤在四面体OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，D为BC的中点，E为AD的中点，则
OE
=
1
2
a
+
1
4
b
+
1
4
c

⑥椭圆
x2
25
+
y2
9
=1上一点P到一个焦点的距离为5，则P到另一个焦点的距离为5．
其中真命题的序号是：
①②③⑤⑥
①②③⑤⑥
．
△ABC中，三个内角A、B、C所对的边分别为a、b、c，设复数z=sinA（sinA-sinC）+（sin2B-sin2C）i，且z在复平面内所对应的点在直线y=x上．
（1）求角B的大小；
（2）若sinB=cosAsinC，△ABC的外接圆的面积为4π，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网