题目内容
12.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2,则e1+e2的取值范围是$(\frac{4}{3},+∞)$.分析 如图所示,设椭圆与双曲线的标准方程分别为:$\frac{{x}^{2}}{{a}_{1}^{2}}+\frac{{y}^{2}}{{b}_{1}^{2}}=1$,$\frac{{x}^{2}}{{a}_{2}^{2}}-\frac{{y}^{2}}{{b}_{2}^{2}}=1$.(a1,a2,b1,b2>0,a1>b1).根据△PF1F2是以PF1为底边的等腰三角形,|PF1|=10,可得10+2c=2a1,10-2c=2a2,可得$2=\frac{1}{{e}_{1}}-\frac{1}{{e}_{2}}$,于是e1+e2=e2+$\frac{{e}_{2}}{2{e}_{2}+1}$=f(e2),e2>1.利用导数研究其单调性即可得出.
解答 解:如图所示,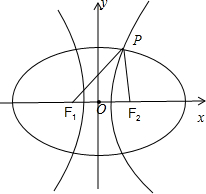
设椭圆与双曲线的标准方程分别为:$\frac{{x}^{2}}{{a}_{1}^{2}}+\frac{{y}^{2}}{{b}_{1}^{2}}=1$,$\frac{{x}^{2}}{{a}_{2}^{2}}-\frac{{y}^{2}}{{b}_{2}^{2}}=1$.(a1,a2,b1,b2>0,a1>b1)
∵△PF1F2是以PF1为底边的等腰三角形,|PF1|=10,
∴10+2c=2a1,10-2c=2a2,
相减可得:2c=a1-a2,
∴$2=\frac{1}{{e}_{1}}-\frac{1}{{e}_{2}}$,
∴${e}_{1}=\frac{{e}_{2}}{2{e}_{2}+1}$,
∴e1+e2=e2+$\frac{{e}_{2}}{2{e}_{2}+1}$=f(e2),e2>1.
∴f′(e2)=1+$\frac{2{e}_{2}+1-2{e}_{2}}{(2{e}_{2}+1)^{2}}$=1+$\frac{1}{(2{e}_{2}+1)^{2}}$>0,
∴函数f(e2)在e2>1时单调递增,
∴f(e2)>f(1)=1+$\frac{1}{3}$=$\frac{4}{3}$.
∴e1+e2的取值范围是$(\frac{4}{3},+∞)$.
故答案为:$(\frac{4}{3},+∞)$.
点评 本题考查了椭圆与双曲线的标准方程及其性质、离心率计算公式、利用导数研究函数的单调性极值,考查了推理能力与计算能力,属于难题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案| A. | x-y+1=0 | B. | 3x+y+7=0 | C. | x+y+3=0 | D. | x-3y-1=0 |
| A. | 4 | B. | 9 | C. | 16 | D. | 25 |
| A. | (x+8)(x2+2x+3)<2 | B. | x+8<2(x2+2x+3) | C. | $\frac{1}{{{x^2}+2x+3}}$<$\frac{2}{x+8}$ | D. | $\frac{{{x^2}+2x+3}}{x+8}$>$\frac{1}{2}$ |
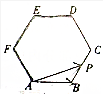 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].