题目内容
若数列{xn}满足lgxn+1=1+lgxn(n∈N*),且x1+x2+…+x100=100,则lg(x101+x102+…+x200)的值为分析:由题意知lgxn+1-lgxn=1,∴lg
=1,所以lg(x101+x102+…+x200)=lg[(x1+x2+…+x100)×10100],由此可求出x1+x2+…+x100=100,则lg(x101+x102+…+x200)的值.
| xn+1 |
| xn |
解答:解:∵lgxn+1-lgxn=1,∴lg
=1,
∴lg(x101+x102+…+x200)
=lg[(x1+x2+…+x100)×10100]
=lg(100×10100)
=lg10102
=102
答案:102.
| xn+1 |
| xn |
∴lg(x101+x102+…+x200)
=lg[(x1+x2+…+x100)×10100]
=lg(100×10100)
=lg10102
=102
答案:102.
点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

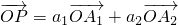 ,求a1+a2的值;
,求a1+a2的值;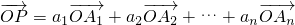 ,我们称
,我们称 是向量
是向量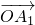 ,
, ,…,
,…,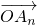 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当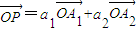 ,求a1+a2的值;
,求a1+a2的值;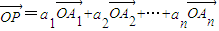 ,我们称
,我们称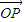 是向量
是向量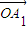 ,
,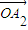 ,…,
,…,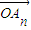 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当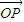 是向量
是向量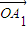 ,
,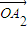 ,…,
,…,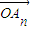 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索: