题目内容
已知集合A={x|x2-4x+3=0},B={x|x2-ax+9=0},若A∪B=A,求实数a的取值范围.
解:由x2-4x+3=0,解得x=1或3,∴A={1,3}.
∵A∪B=A,∴B?A,或B=A.
①若B=A,则必有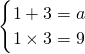 ,无解,应舍去;
,无解,应舍去;
②若B?A,则B可能为∅,{1},{3}.
当B=∅时,△=a2-36<0,解得-6<a<6;
当B={1}或{3}时,要求△=a2-36=0,即a=±6,且1或3必是方程x2-ax+9=0,的重根.
只有a=6时,B={3}适合,而a=-6时不适合,应舍去.
综上可知:实数a的取值范围是(-6,6].
故答案为(-6,6].
分析:由A∪B=A,可得B?A,或B=A.分类讨论即可.
点评:正确理解集合间的关系和恰当分类是解题的关键.
∵A∪B=A,∴B?A,或B=A.
①若B=A,则必有
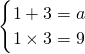 ,无解,应舍去;
,无解,应舍去;②若B?A,则B可能为∅,{1},{3}.
当B=∅时,△=a2-36<0,解得-6<a<6;
当B={1}或{3}时,要求△=a2-36=0,即a=±6,且1或3必是方程x2-ax+9=0,的重根.
只有a=6时,B={3}适合,而a=-6时不适合,应舍去.
综上可知:实数a的取值范围是(-6,6].
故答案为(-6,6].
分析:由A∪B=A,可得B?A,或B=A.分类讨论即可.
点评:正确理解集合间的关系和恰当分类是解题的关键.

练习册系列答案
相关题目