题目内容
设0≤α≤π,不等式8x2-(8sinα)x+cos2α≥0对x∈R恒成立,则α的取值范围为______.
由题意可得,△=64sin2α-32cos2α≤0,
得2sin2α-(1-2sin2α)≤0
∴sin2α≤
,
-
≤sinα≤
,
∵0≤α≤π
∴α∈[0,
]∪[
,π].
故答案为:[0,
]∪[
,π].
得2sin2α-(1-2sin2α)≤0
∴sin2α≤
| 1 |
| 4 |
-
| 1 |
| 2 |
| 1 |
| 2 |
∵0≤α≤π
∴α∈[0,
| π |
| 6 |
| 5π |
| 6 |
故答案为:[0,
| π |
| 6 |
| 5π |
| 6 |

练习册系列答案
相关题目
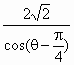 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.