题目内容
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB、FC.
(Ⅰ)求证:FB=FC;
(Ⅱ)求证:FB2=FA·FD;
(Ⅲ)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6cm,求AD的长.
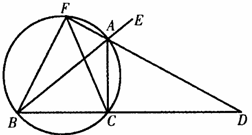
解:(Ⅰ)∵AD平分ÐEAC,∴ÐEAD=ÐDAC.
∵四边形AFBC内接于圆,∴ÐDAC=ÐFBC.
∵ÐEAD=ÐFAB=ÐFCB,∴ÐFBC=ÐFCB,∴FB=FC. ……………………3分
(Ⅱ)∵ÐFAB=ÐFCB=ÐFBC ,ÐAFB=ÐBFD,
∴ΔFBA∽ΔFDB.∴![]() ,∴ FB2=FA·FD. …………………………6分
,∴ FB2=FA·FD. …………………………6分
(Ⅲ)∵AB是圆的直径,∴ÐACB=90°.
∵ÐEAC=120°, ∴ÐDAC=![]() ÐEAC=60°,ÐBAC=60°.∴ÐD=30°.
ÐEAC=60°,ÐBAC=60°.∴ÐD=30°.
∵BC= 6, ∴AC=![]() . ∴AD=2AC=
. ∴AD=2AC=![]() cm.……………………………10分
cm.……………………………10分

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知AD∥BE∥CF,下列比例式成立的是( )
如图,已知AD∥BE∥CF,下列比例式成立的是( ) 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2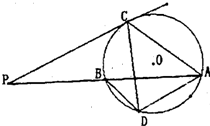 (2011•洛阳二模)如图,已知PBA是圆O的割线,PC是圆的切线,
(2011•洛阳二模)如图,已知PBA是圆O的割线,PC是圆的切线,