题目内容
设 ,其中a为正实数.
,其中a为正实数.
(1)当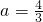 时,求f(x)的极值点;
时,求f(x)的极值点;
(2)若f(x)为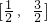 上的单调函数,求a的取值范围.
上的单调函数,求a的取值范围.
解:∵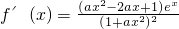 ,
,
(1)当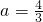 时,若f'(x)=0,
时,若f'(x)=0,
则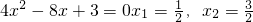 ,
,
∴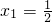 是极大值点,
是极大值点,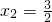 是极小值点;
是极小值点;
(2)记g(x)=ax2-2ax+1,则g(x)=a(x-1)2+(1-a),
∵f(x)为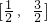 上的单调函数,
上的单调函数,
则f'(x)在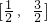 上不变号,
上不变号,
∵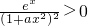 ,
,
∴g(x)≥0或g(x)≤0对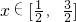 恒成立,
恒成立,
由g(1)≥0或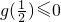 ?0<a≤1或
?0<a≤1或 ,
,
∴a的取值范围是0<a≤1或 .
.
分析:(1)把a= 代入
代入 ,对f(x)进行求导,令f′(x)=0,解出其极值点;
,对f(x)进行求导,令f′(x)=0,解出其极值点;
(2)已知f(x)上的为单调函数,可知f′(x)在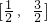 恒大于等于0,或恒小于等于0,利用求出a的取值范围.
恒大于等于0,或恒小于等于0,利用求出a的取值范围.
点评:此题主要考查利用导数求函数的单调性,解此题的关键是对f(x)能够正确求导,利用了转化的思想,是一道中档题;
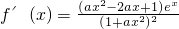 ,
,(1)当
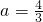 时,若f'(x)=0,
时,若f'(x)=0,则
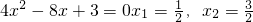 ,
,| x | 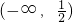 |  | 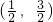 |  | 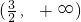 |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
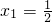 是极大值点,
是极大值点,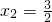 是极小值点;
是极小值点; (2)记g(x)=ax2-2ax+1,则g(x)=a(x-1)2+(1-a),
∵f(x)为
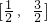 上的单调函数,
上的单调函数,则f'(x)在
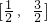 上不变号,
上不变号,∵
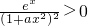 ,
,∴g(x)≥0或g(x)≤0对
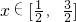 恒成立,
恒成立,由g(1)≥0或
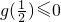 ?0<a≤1或
?0<a≤1或 ,
,∴a的取值范围是0<a≤1或
 .
.分析:(1)把a=
 代入
代入 ,对f(x)进行求导,令f′(x)=0,解出其极值点;
,对f(x)进行求导,令f′(x)=0,解出其极值点;(2)已知f(x)上的为单调函数,可知f′(x)在
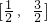 恒大于等于0,或恒小于等于0,利用求出a的取值范围.
恒大于等于0,或恒小于等于0,利用求出a的取值范围.点评:此题主要考查利用导数求函数的单调性,解此题的关键是对f(x)能够正确求导,利用了转化的思想,是一道中档题;

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ,其中a为正实数。
,其中a为正实数。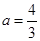 时,求
时,求 的极值点;
的极值点; ,其中a为正实数,
,其中a为正实数, 的极值点;
的极值点; 为R上的单调函数,求a的取值范围。
为R上的单调函数,求a的取值范围。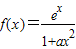 ,其中a为正实数
,其中a为正实数 时,求f(x)的极值点;
时,求f(x)的极值点; ,其中a为正实数
,其中a为正实数 时,求f(x)的极值点;
时,求f(x)的极值点; ,其中a为正实数
,其中a为正实数 时,求f(x)的极值点;
时,求f(x)的极值点;