题目内容
 (2011•洛阳一模)如图,在底面是正方形的四棱锥P-ABCD中;PA⊥AC上一点.
(2011•洛阳一模)如图,在底面是正方形的四棱锥P-ABCD中;PA⊥AC上一点.(1)确定点G的位置,使FG∥平面PBD,并说明理由;
(2)当二面角B-PC-D的大小为120°时,求PC与底面ABCD所成角的正切值.
分析:(1)G是EC的中点,利用三角形中位线的性质,证明FG∥PE,利用线面平行的判定定理,即可得到结论;
(2)过B作BH⊥PC,垂足为H,连接DH,证明∠BHD是二面角B-PC-D的平面角,从而可求PC与底面ABCD所成角的正切值.
(2)过B作BH⊥PC,垂足为H,连接DH,证明∠BHD是二面角B-PC-D的平面角,从而可求PC与底面ABCD所成角的正切值.
解答: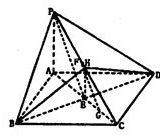 解:(1)G是EC的中点,证明如下
解:(1)G是EC的中点,证明如下
连接PE,因为G是EC的中点,F是PC的中点,
∴FG∥PE,
∵PE?平面PBD,FG?平面PBD,
∴FG∥平面PBD,
(2)过B作BH⊥PC,垂足为H,连接DH,
由已知△PBC≌△PDC,
∴∠BCH=∠DCH,
∴△BCH≌△DCH,
∴DH⊥PC,
∴∠BHD是二面角B-PC-D的平面角.
设底面边长为a,则BD2=2BH2-2BH2cos∠BHD,
∴BH=
a,
∵PB•BC=PC•BH,
∴
•a=
•
a,
∴PA=a,
在Rt△PCA中,tan∠PCA=
=
=
,
即PC与底面ABCD所成角的正切值
.
 解:(1)G是EC的中点,证明如下
解:(1)G是EC的中点,证明如下连接PE,因为G是EC的中点,F是PC的中点,
∴FG∥PE,
∵PE?平面PBD,FG?平面PBD,
∴FG∥平面PBD,
(2)过B作BH⊥PC,垂足为H,连接DH,
由已知△PBC≌△PDC,
∴∠BCH=∠DCH,
∴△BCH≌△DCH,
∴DH⊥PC,
∴∠BHD是二面角B-PC-D的平面角.
设底面边长为a,则BD2=2BH2-2BH2cos∠BHD,
∴BH=
| ||
| 3 |
∵PB•BC=PC•BH,
∴
| a2+PA2 |
| 2a2+PA2 |
| ||
| 3 |
∴PA=a,
在Rt△PCA中,tan∠PCA=
| PA |
| AC |
| a | ||
|
| ||
| 2 |
即PC与底面ABCD所成角的正切值
| ||
| 2 |
点评:本题考查线面平行,考查线面角,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2011•洛阳一模)如图,是一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积( )
(2011•洛阳一模)如图,是一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积( )