题目内容
已知双曲线(1)求双曲线的方程;
(2)设A(m,0),B(![]() ,0)(0<m<1)是x轴上的两点,过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,设直线BC交双曲线于另一点E,证明:直线DE垂直于x轴.
,0)(0<m<1)是x轴上的两点,过点A作斜率不为0的直线l,使得l交双曲线于C、D两点,设直线BC交双曲线于另一点E,证明:直线DE垂直于x轴.
答案:(1)∵e=![]() ,得c=
,得c=![]() a,b=
a,b=![]() a,
a,
又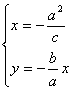 ,解得M(
,解得M(![]() ),
),
而![]() .
.
即![]() a2-c2+
a2-c2+![]() a2=a2-c2=
a2=a2-c2=![]() ,
,
解得a2=1,b2=![]() ,
,
∴所求双曲线方程为:x2-4y2=1.
(2)设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l:y=![]() (x-m),
(x-m),
则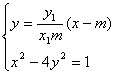 ,且
,且![]() =1
=1
得(![]() -2x1m+m2
-2x1m+m2![]() )x2+8m
)x2+8m![]()
![]() m2
m2![]() +2mx1-m2=0
+2mx1-m2=0
即(m2-2x1m+1)x2+8m![]() -(
-(![]() -2mx1+m2
-2mx1+m2![]() )=0,且m2-2x1m+1
)=0,且m2-2x1m+1![]() 0,
0,
于是x1x2=![]() ,
,
即x2=![]() ,
,
同理可得x3=![]() (将上式中的m用
(将上式中的m用![]() 代替)
代替)
∴x2=x3,即直线DE垂直于x轴.

练习册系列答案
相关题目