Question

【题目】若是各项均为正数的数列的前项和，且.

（1）求的值；

（2）设，且数列的前项和满足对任意正整数恒成立，求实数的取值范围；

（3）设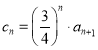，问：是否存在正整数，使得对一切正整数恒成立？若存在，请求出实数的值；若不存在，请说明理由.

Answer 1

【答案】（1），；（2）或；（3）存在，

【解析】

（1）令，可求出，令，可求出，进而可求得的值；

（2）先求出的表达式，进而可求出的表达式，再结合，可求出，并得到，从而可知，即可求出的取值范围；

（3）由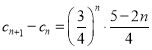，可知当时，，当时，，从而可知时，对一切正整数恒成立.

（1）当时，，解得，

因为数列各项均为正数，所以.

当时，，又，解得，

由，解得.

（2）因为，

所以，又，所以.

当时，，

当时，.

时也符合上式，所以.

则，

所以.

所以，解得或.

（3）因为，

所以.

当时，，所以，

当时，，所以.

所以时，对一切正整数恒成立.