题目内容
如图,已知梯形ABCD中,CD=2,AC=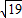 ,∠BAD=60°,求
,∠BAD=60°,求(1)边AD的长度
(2)梯形的高.
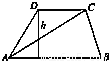
【答案】分析:(1)在三角形ACD中,利用余弦定理列出关系式,将AC,CD及cos∠ADC的值代入计算即可求出AD的长;
(2)利用锐角三角函数定义即可求出梯形的高.
解答:解:(1)∵CD=2,AC=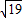 ,∠BAD=60°,即∠ADC=120°,
,∠BAD=60°,即∠ADC=120°,
∴在△ACD中,AC2=AD2+CD2-2AD•CD•cos120°,
∴AD2+2AD-15=0,
∴AD=3或AD=-5(舍去),
(2)∵AD=3,∴h=AD•sin60°=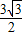 .
.
点评:此题考查了余弦定理,锐角三角函数定义,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.
(2)利用锐角三角函数定义即可求出梯形的高.
解答:解:(1)∵CD=2,AC=
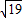 ,∠BAD=60°,即∠ADC=120°,
,∠BAD=60°,即∠ADC=120°,∴在△ACD中,AC2=AD2+CD2-2AD•CD•cos120°,
∴AD2+2AD-15=0,
∴AD=3或AD=-5(舍去),
(2)∵AD=3,∴h=AD•sin60°=
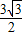 .
.点评:此题考查了余弦定理,锐角三角函数定义,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
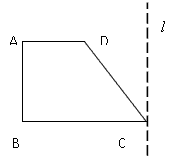
 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.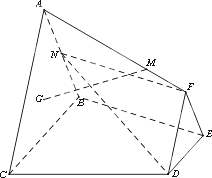

 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。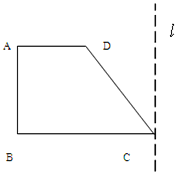 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.