题目内容
已知向量 ,
, ,且
,且 .
.
(1)求 及
及 ;
;
(2)若 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
(1)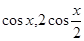 ;(2)
;(2)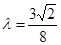 .
.
解析试题分析:解题思路:(1)利用平面向量的数量积公式、模长公式求解;(2)将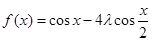 的值域,转化为关于
的值域,转化为关于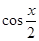 的一元二次函数的值域.规律总结:1.三角恒等变换要正确选用公式及其变形;2.求关于
的一元二次函数的值域.规律总结:1.三角恒等变换要正确选用公式及其变形;2.求关于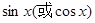 的一元二次函数的值域,要注意三角函数的有界性.
的一元二次函数的值域,要注意三角函数的有界性.
试题解析:(1)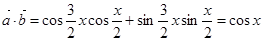 ,
,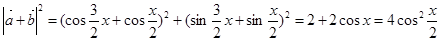 ,
,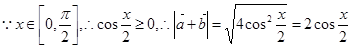 .
.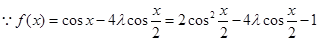 ,
,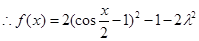 ,
,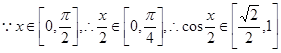 ,
,
当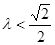 时,当且仅当
时,当且仅当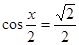 时,
时, 取最小值
取最小值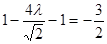 ,解得
,解得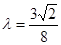 ;
;
当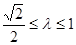 时,当且仅当
时,当且仅当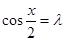 时,
时, 取最小值
取最小值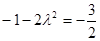 ,解得
,解得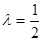 (舍);
(舍);
当 时,当且仅当
时,当且仅当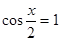 时,
时, 取最小值
取最小值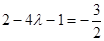 ,解得
,解得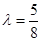 (舍去),
(舍去),
综上所述,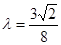 .
.
考点:1.平面向量的数量积;2.一元二次函数的值域;3.分类讨论思想.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
 ,
,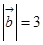 ,
,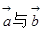 的夹角为θ,且tanθ=
的夹角为θ,且tanθ=
 的值; (2)求
的值; (2)求 的值.
的值. =(1,2),
=(1,2), =(-2,n) (n>1),
=(-2,n) (n>1), 与
与 |=4,|
|=4,| |=3,(2
|=3,(2 的夹角θ;
的夹角θ; ,求以
,求以 为邻边的平行四边形的两条对角线的长度.
为邻边的平行四边形的两条对角线的长度. ·
· =
=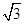 |
| |2,求角A,B,C的大小.
|2,求角A,B,C的大小. (a>b>0)经过点M(
(a>b>0)经过点M( ,1),离心率为
,1),离心率为 .
. ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由. ,
, ,
, .
. ,求
,求 的值;
的值; ,若
,若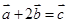 ,求
,求 、
、 的值.
的值. 的正方形
的正方形 的边长为2,点
的边长为2,点 、
、 分别为线段
分别为线段 、
、 上的两个不同点,且
上的两个不同点,且 ,则
,则 的取值范围是
的取值范围是