题目内容
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知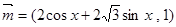 ,
,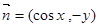 ,满足
,满足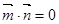 .
.
(1)将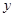 表示为
表示为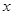 的函数
的函数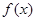 ,并求
,并求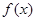 的最小正周期;
的最小正周期;
(2)已知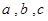 分别为
分别为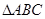 的三个内角
的三个内角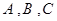 对应的边长,若
对应的边长,若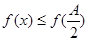 对所有
对所有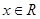 恒成立,且
恒成立,且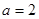 ,求
,求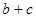 的取值范围.
的取值范围.
(I) ,其最小正周期为
,其最小正周期为 . (II)
. (II)
解析试题分析:(I)由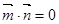 得
得
即

所以 ,其最小正周期为
,其最小正周期为 .
.
(II)因为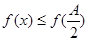 对所有
对所有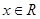 恒成立
恒成立
所以 ,且
,且
因为 为三角形内角,所以
为三角形内角,所以 ,所以
,所以 .
.
由正弦定理得 ,
, ,
,


 ,
, ,
,
所以 的取值范围为
的取值范围为
考点:本题考查了三角函数的性质及正余弦定理
点评:此类问题比较综合,运用时除了掌握三角函数的恒等变换之外,还要求灵活运用正余弦定理

练习册系列答案
相关题目
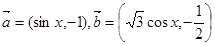 ,函数
,函数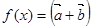 ·
·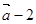
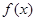 的最小正周期T及单调减区间
的最小正周期T及单调减区间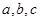 分别是△ABC内角A,B,C的对边,其中A为锐角,
分别是△ABC内角A,B,C的对边,其中A为锐角,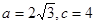 且
且 ,求A,b和△ABC的面积S
,求A,b和△ABC的面积S 为坐标原点,向量
为坐标原点,向量 ,
, ,
, 点
点 是直线
是直线 上一点,且
上一点,且 ;
; ,
,  ,讨论
,讨论 的单调性,并求其值域;
的单调性,并求其值域; 共线,求
共线,求 的值。
的值。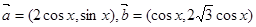 ,函数
,函数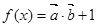 .
. 的单调递增区间;
的单调递增区间; 中,
中,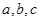 分别是角
分别是角 的对边,
的对边,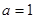 且
且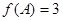 ,求
,求 的最大值.
的最大值. 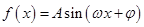
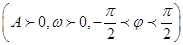 一个周期的图像如图所示。
一个周期的图像如图所示。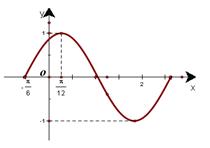
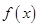 的表达式;
的表达式;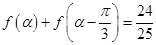 ,且
,且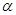 为
为 的一个内角,求
的一个内角,求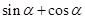 的值。
的值。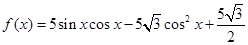 ,(Ⅰ)确定函数
,(Ⅰ)确定函数 的单调增区间;(Ⅱ)当函数
的单调增区间;(Ⅱ)当函数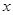 的集合.
的集合. ,
, ,设函数
,设函数 .
.  的零点组成公差为
的零点组成公差为 的等差数列,求函数
的等差数列,求函数 ,(
,( ),求函数
),求函数 。
。 的周期和及其图象的对称中心;
的周期和及其图象的对称中心; ,满足
,满足 求函数
求函数 的取值范围。
的取值范围。 .
. 的最小正周期,最大值及取最大值时相应的
的最小正周期,最大值及取最大值时相应的 值;
值; ,求
,求