题目内容
若函数f(x)="sin" 2xcos +cos 2x sin
+cos 2x sin (x∈R),其中
(x∈R),其中 为实常数,且f(x)≤f(
为实常数,且f(x)≤f( )对任意实数R恒成立,记p=f(
)对任意实数R恒成立,记p=f( ),q=f(
),q=f( ),r=f(
),r=f( ),则p、q、r的大小关系是( )
),则p、q、r的大小关系是( )
| A.r<p<q | B.q<r<p | C.p<q<r | D.q<p<r |
C
解析试题分析: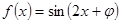 ,当
,当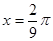 时,函数取得最大值,函数的最小正周期
时,函数取得最大值,函数的最小正周期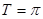 ,根据周期和对称性知
,根据周期和对称性知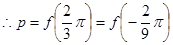 ,
,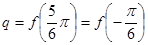 ,
,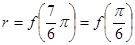 ,
,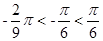 位于函数的增区间,所以
位于函数的增区间,所以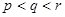 ,故选C.
,故选C.
考点:1.三角函数的性质;2.比较大小.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
已知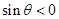 ,
,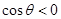 ,则角
,则角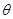 的终边所在的象限是( )
的终边所在的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下面的函数中,周期为 的偶函数是
的偶函数是
A. | B. | C. | D. |
半径为3,中心角为120o的扇形面积为( ).
A.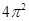 | B.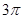 | C.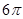 | D.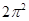 |
已知向量 ,向量
,向量 ,则
,则 的最大值、最小值分别是( ).
的最大值、最小值分别是( ).
A. | B. | C. | D. |
已知 ,则
,则 ( )
( )
| A.3 | B. | C. | D. |
在[0,2 ]内,满足sinx>cosx的x的取值范围是( )
]内,满足sinx>cosx的x的取值范围是( )
A.( , , ) ) | B.( , , ) ) | C.( , , ) ) | D.( , , ) ) |
 变为曲线
变为曲线 的伸缩变换是( )
的伸缩变换是( )



 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的函数图象,则下列说法正确的是 ( )
的函数图象,则下列说法正确的是 ( )