题目内容
已知三角形ABC的顶点分别为A(-3,0)、B(9,5)、C(3,9),直线l经过C把三角形的面积为1:2两部分,求直线l的方程.
解:设直线l与线段AB的交点为D,则A、B两点到直线直线l 的距离之比等于1:2或 2:1,
当直线l的斜率不存在时,直线l的方程为 x=3,A到直线l的距离为6,B到直线l的距离为 6,不满足条件.
当直线l的斜率存在时,设直线l的方程为 y-9=k(x-3),即 kx-y+9-3k=0,
由题意知,k≥kCA,或 k≤KCB,∴k≥ =
= ,或 k≤
,或 k≤ =-
=- .
.
即k≥ ,或 k≤-
,或 k≤- .
.
A到直线l的距离为 =
= ,B到直线l的距离为
,B到直线l的距离为 =
= ,
,
由题意得 =
= ,或
,或  =2,解得 k=
=2,解得 k= 或 k=-
或 k=-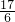 .
.
故直线l的方程为 ,或-
,或- .
.
即11x-3y-6=0或17x+6y-105=0,
故直线l的方程为11x-3y-6=0,或17x+6y-105=0.
分析:当直线l的斜率不存在时,经检验不满足条件. 当直线l的斜率存在时,由 k≥kCA,或 k≤KCB,求出k 的范围,求出A、B两点到直线直线l 的距离,由A、B两点到直线直线l 的距离之比等于1:2或 2:1,求出k值,用点斜式求得直线l的方程.
点评:本题考查用点斜式求直线方程的方法,点到直线的距离公式的应用,求出直线l的斜率k 的范围是解题的难点和关键.
当直线l的斜率不存在时,直线l的方程为 x=3,A到直线l的距离为6,B到直线l的距离为 6,不满足条件.
当直线l的斜率存在时,设直线l的方程为 y-9=k(x-3),即 kx-y+9-3k=0,
由题意知,k≥kCA,或 k≤KCB,∴k≥
 =
= ,或 k≤
,或 k≤ =-
=- .
.即k≥
 ,或 k≤-
,或 k≤- .
.A到直线l的距离为
 =
= ,B到直线l的距离为
,B到直线l的距离为 =
= ,
,由题意得
 =
= ,或
,或  =2,解得 k=
=2,解得 k= 或 k=-
或 k=-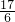 .
.故直线l的方程为
 ,或-
,或- .
.即11x-3y-6=0或17x+6y-105=0,
故直线l的方程为11x-3y-6=0,或17x+6y-105=0.
分析:当直线l的斜率不存在时,经检验不满足条件. 当直线l的斜率存在时,由 k≥kCA,或 k≤KCB,求出k 的范围,求出A、B两点到直线直线l 的距离,由A、B两点到直线直线l 的距离之比等于1:2或 2:1,求出k值,用点斜式求得直线l的方程.
点评:本题考查用点斜式求直线方程的方法,点到直线的距离公式的应用,求出直线l的斜率k 的范围是解题的难点和关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 在三角形内部及
在三角形内部及 的最大值和最小值分别是 ( )
的最大值和最小值分别是 ( )