题目内容
命题p：关于x的不等式x2+2ax+4＞0，对一切x∈R恒成立，命题q：函数f（x）=（3-2a）x是增函数，若p∨q为真，p∧q为假，求实数a的取值范围．
【答案】分析：由p∨q为真，p∧q为假，知p为真，q为假，或p为假，q为真．由此利用二元一次不等式和指数函数的性质，能求出实数a的取值范围．
解答：解：∵p∨q为真，p∧q为假，∴p为真，q为假，或p为假，q为真．
①当p为真，q为假时，
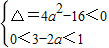，解得1＜a＜2．
②当p为假，q为真时，
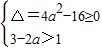，解得a≤-2
综上，实数a的取值范围是{a|a≤-2或1＜a＜2}．
点评：本题考查命题的真假判断，是基础题．解题时要认真审题，仔细解答．
解答：解：∵p∨q为真，p∧q为假，∴p为真，q为假，或p为假，q为真．
①当p为真，q为假时，
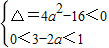，解得1＜a＜2．②当p为假，q为真时，
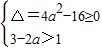，解得a≤-2综上，实数a的取值范围是{a|a≤-2或1＜a＜2}．
点评：本题考查命题的真假判断，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目