Question

若函数f（x），g（x）分别是R上的偶函数、奇函数，且满足f（x）-g（x）=e^x，则g（f（0））=________．

Answer 1

分析：依题意可求得f（x）=，g（x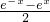）=，从而可求得g（f（0））的值．
解答：∵f（x）-g（x）=e^x，①
∴f（-x）-g（-x）=e^-x，
又函数f（x），g（x）分别是R上的偶函数、奇函数，
∴f（x）+g（x）=e^-x，②
①②联立可得，f（x）=，g（x）=，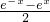
∴f（0）=1，
∴g（f（0））=g（1）==．
故答案为：．
点评：本题考查函数奇偶性的性质，理解函数的奇偶性布列方程组是关键，考查解方程组的能力，属于中档题．