题目内容
3．△ABC的内角A、B、C所对的边分别为a、b、c，且满足（a+b+c）（a-b+c）=4，若A、B、C成等差数列，则ac的值为$\frac{4}{3}$．分析 由三角形三个内角成等差数列，利用等差数列的性质求出B的度数，利用余弦定理表示出cosB，将B的度数代入整理得到关系式，已知等式变形后代入计算求出ac的值即可．
解答 解：∵△ABC中，A、B、C成等差数列，且A+B+C=π，
∴2B=A+C=π-B，即B=$\frac{π}{3}$，
∴由余弦定理得：cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$，即a2+c2-b2=ac，
∵（a+b+c）（a-b+c）=（a+c）2-b2=a2+c2-b2+2ac=4，
∴ac+2ac=4，即ac=$\frac{4}{3}$，
故答案为：$\frac{4}{3}$
点评 此题考查了余弦定理，等差数列的性质，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
11．
2011年3月11日，日本发生了9.0级大地震，同时导致了福岛核电站的泄露事件，给环境带来的一定的污染，也给世界各国的人们对环境的保护敲响了警钟．根据空气质量指数API（为整数）的不同，可将空气质量分级如表：
某环境部门对一城市一年（365天）的空气质量进行检测，获得的API数据按照区间[0，50]，（50，100]，（100，150]，（150，200]，（200，250]，（250，300]进行分组，得到频率分布直方图如下图：
（1）求直方图中x的值；
（2）计算一年中空气质量为良和轻微污染的总天数；
（3）求该城市一年中每天空气质量不为良且不为轻微污染的概率．
2011年3月11日，日本发生了9.0级大地震，同时导致了福岛核电站的泄露事件，给环境带来的一定的污染，也给世界各国的人们对环境的保护敲响了警钟．根据空气质量指数API（为整数）的不同，可将空气质量分级如表：| API | 0～50 | 51～200 | 101～150 | 151～200 | 201～250 | 251～300 | ＞300 |
| 级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
（1）求直方图中x的值；
（2）计算一年中空气质量为良和轻微污染的总天数；
（3）求该城市一年中每天空气质量不为良且不为轻微污染的概率．
18．下列函数中，在其定义域内既是偶函数又在（-∞，0）上单调递增的函数是（ ）
| A． | f（x）=x2 | B． | f（x）=-log2|x| | C． | f（x）=3|x| | D． | f（x）=sinx |
8．为得到函数y=sin（x+$\frac{π}{6}$）的图象，可将函数y=sinx的图象向左平移m个单位长度，或向右平移n个单位长度（m，n均为正数，则|m-n|的最小值是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | π | D． | 2π |
15．执行如图所示的程序框图，输出的结果为（ ）
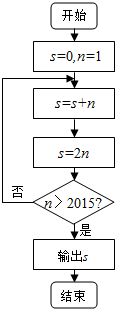
| A． | 210-1 | B． | 211-1 | C． | 21007-1 | D． | 21024-1 |
12．在极坐标系中，曲线C：ρ=2sinθ，A、B为曲线C的两点，以极点为原点，极轴为x轴非负半轴的直角坐标中，曲线E：$\left\{{\begin{array}{l}{x=4t+2}\\{y=-3t-3}\end{array}}\right.$上一点P，则∠APB的最大值为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |
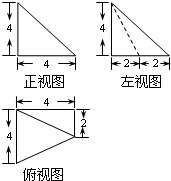
如图，在四棱锥O-ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA=2，M为OA的中点．则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$．