题目内容
下列命题中,正确的命题有
①用相关系数r来判断两个变量的相关性时,r越接近0,说明两个变量有较强的相关性;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量ξ服从正态分布N(0,1),若 ;
;
④回归直线一定过样本点的中心 .
.
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:①两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值越接近于0,表示两个变量之间几乎不存在线性相关;②根据方差公式可知方差恒不变;③根据正态分布N(0,1)的密度函数的图象对称性可得,P(-1<ξ<0)=P(0<ξ<1);④根据线性回归方程可知回归直线一定过样本点的中心 ,由此可得结论.
,由此可得结论.
解答:①两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值越接近于0,表示两个变量之间几乎不存在线性相关,故①不正确;
②将一组数据中的每个数据都加上或减去同一个常数后,根据方差公式可知方差恒不变,故②正确;
③根据正态分布N(0,1)的密度函数的图象对称性可得,P(-1<ξ<0)=P(0<ξ<1)=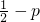 ,故③正确;
,故③正确;
④根据线性回归方程可知回归直线一定过样本点的中心 ,故④正确.
,故④正确.
故选C.
点评:本题考查线性回归方程,考查正态分布,考查方差,明确概念,正确计算是关键.
分析:①两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值越接近于0,表示两个变量之间几乎不存在线性相关;②根据方差公式可知方差恒不变;③根据正态分布N(0,1)的密度函数的图象对称性可得,P(-1<ξ<0)=P(0<ξ<1);④根据线性回归方程可知回归直线一定过样本点的中心
 ,由此可得结论.
,由此可得结论.解答:①两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值越接近于0,表示两个变量之间几乎不存在线性相关,故①不正确;
②将一组数据中的每个数据都加上或减去同一个常数后,根据方差公式可知方差恒不变,故②正确;
③根据正态分布N(0,1)的密度函数的图象对称性可得,P(-1<ξ<0)=P(0<ξ<1)=
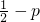 ,故③正确;
,故③正确;④根据线性回归方程可知回归直线一定过样本点的中心
 ,故④正确.
,故④正确.故选C.
点评:本题考查线性回归方程,考查正态分布,考查方差,明确概念,正确计算是关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命
。则下列四个命 是以4为周期的周期函数; ②
是以4为周期的周期函数; ② 上的解析式为
上的解析式为 ;
; ; ④
; ④ 处的切线方程为
处的切线方程为 。
。 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足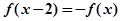 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命
。则下列四个命 是以4为周期的周期函数; ②
是以4为周期的周期函数; ② 上的解析式为
上的解析式为 ;
; ; ④
; ④ 处的切线方程为
处的切线方程为 。
。