题目内容
已知函数
(1)求函数 的单调区间.
的单调区间.
(2)若方程 有4个不同的实根,求
有4个不同的实根,求 的范围?
的范围?
(3)是否存在正数 ,使得关于
,使得关于 的方程
的方程 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由.
(1)增区间为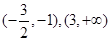 ,减区间为
,减区间为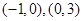 ;(2)
;(2) ;(3)不存在,理由见详解.
;(3)不存在,理由见详解.
解析试题分析:(1)首先求导函数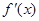 ,然后通过判断
,然后通过判断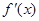 的符号可求得单调区间;(2)构造函数
的符号可求得单调区间;(2)构造函数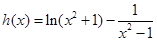 ,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函
,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函 的取值范围;(3)
的取值范围;(3)
试题解析:(1)根据 定义域后,求导得到
定义域后,求导得到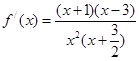 ,
,
根据导数和0的关系得到在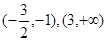 是函数
是函数 的增区间;在
的增区间;在 是函数
是函数 减区间.
减区间.
(2)(2)令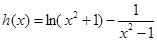 ,求导得
,求导得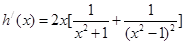 ,
,
里面有一个零点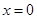 和两个断点
和两个断点 ,所以初步可以得到函数在区间
,所以初步可以得到函数在区间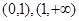 单调增;在区间
单调增;在区间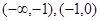 单调减.
单调减.
当 从负半轴方向趋近于-1时,
从负半轴方向趋近于-1时,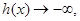
当 从正半轴方向趋近于-1时,
从正半轴方向趋近于-1时,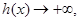
而且 时,
时,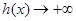 ,
,
而且可以很容易得到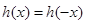 ,函数为偶函数,而且
,函数为偶函数,而且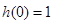 ,
,
另半边的图像就容易模拟得到了,所以 有4个不同的实根,结合图像得到
有4个不同的实根,结合图像得到 .
.
(本题必须另半边如果不分析必须用奇偶性说明;而且必须说明在断点处的趋势,否则扣2到3分)
(3)结论:这样的正数 不存在.
不存在.
假设存在满足条件的 ,使得方程
,使得方程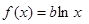 存在两个不相等的实根
存在两个不相等的实根 和
和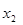 ,然后代入方程,根据其结构利用第(1)问的结论判断出
,然后代入方程,根据其结构利用第(1)问的结论判断出 在
在 上的取值及单调性,然后结合假设导出矛盾,作出判断.
上的取值及单调性,然后结合假设导出矛盾,作出判断.
假设存在正数 ,使得方程
,使得方程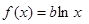 存在两个不相等的实根
存在两个不相等的实根 和
和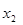 ,则
,则
根据定义域知道 和
和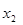 都是正数.
都是正数.
根据第1问知道,当 时,函数的最小值
时,函数的最小值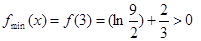 ,
,
所以 ,
,
因为 ,等式两边同号,所以,
,等式两边同号,所以,
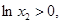 所以
所以

不妨设
由(1)(2)可得 ,
,
所以 ,
,
所以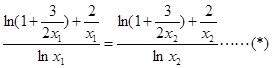 .
.
因为很容易证明到函数 在
在 为恒大于0且为减函数
为恒大于0且为减函数
所以(*)方程显然不成立,因为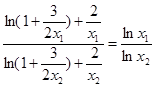 左边大于1,右边小于1.
左边大于1,右边小于1.
所以原假设:存在正数 ,使得方程
,使得方程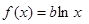 存在两个不相等的实根
存在两个不相等的实根 和
和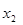 错误(本题其他证法,请酌情给分)
错误(本题其他证法,请酌情给分)
考点:1、导数与函数的单调性关系;2、探索性问题;3、函数与方程根的关系.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案

 的单调性;
的单调性; 时,关于
时,关于 的方程
的方程 有唯一解,求
有唯一解,求 的值;
的值; 时,证明: 对一切
时,证明: 对一切 ,都有
,都有 成立.
成立. 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域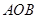 内.分界线
内.分界线 固定,且
固定,且 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足 .
. (
( )百米,
)百米,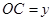 百米.
百米.
 表示成
表示成 的函数,并求出函数
的函数,并求出函数 最小,并求出其面积的最小值.
最小,并求出其面积的最小值. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的图象在区间
的图象在区间 上有公共点,求实数
上有公共点,求实数 的取值范围.
的取值范围. 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数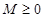 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 ,
, .
. 为奇函数,求实数
为奇函数,求实数 的值;
的值; 上的所有上界构成的集合;
上的所有上界构成的集合; 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数