题目内容
已知数列{an}中a1=1,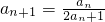 (n∈N+).
(n∈N+).
(1)求证:数列 为等差数列;
为等差数列;
(2)设bn=an•an+1(n∈N+),数列{bn}的前n项和为Sn,求满足 的最小正整数n.
的最小正整数n.
(1)证明:由a1=1与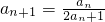 得an≠0,
得an≠0, ,
,
所以对?n∈N+,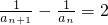 为常数,
为常数,
故 为等差数列;
为等差数列;
(2)解:由(1)得 ,
,
 ,
,
所以 =
=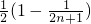 =
= ,
,
由 即
即 ,得
,得 ,
,
所以满足 的最小正整数n=503.
的最小正整数n=503.
分析:(1)对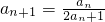 (n∈N+)两边取导数,然后利用等差数列的定义即可证明.
(n∈N+)两边取导数,然后利用等差数列的定义即可证明.
(2)先由(1)求出 ,进而求出an,bn,然后利用列项相消法求出Sn,再解不等式
,进而求出an,bn,然后利用列项相消法求出Sn,再解不等式 即可求得最小整数n;
即可求得最小整数n;
点评:本题考查数列递推式、等差数列的判定及数列求和问题,若{an}为等差数列,公差为d(d≠0),则{ }的前n项和用列项相消法,其中
}的前n项和用列项相消法,其中 =
= .
.
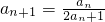 得an≠0,
得an≠0, ,
,所以对?n∈N+,
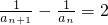 为常数,
为常数,故
 为等差数列;
为等差数列;(2)解:由(1)得
 ,
, ,
,所以
 =
=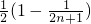 =
= ,
,由
 即
即 ,得
,得 ,
,所以满足
 的最小正整数n=503.
的最小正整数n=503.分析:(1)对
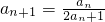 (n∈N+)两边取导数,然后利用等差数列的定义即可证明.
(n∈N+)两边取导数,然后利用等差数列的定义即可证明.(2)先由(1)求出
 ,进而求出an,bn,然后利用列项相消法求出Sn,再解不等式
,进而求出an,bn,然后利用列项相消法求出Sn,再解不等式 即可求得最小整数n;
即可求得最小整数n;点评:本题考查数列递推式、等差数列的判定及数列求和问题,若{an}为等差数列,公差为d(d≠0),则{
 }的前n项和用列项相消法,其中
}的前n项和用列项相消法,其中 =
= .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目