题目内容
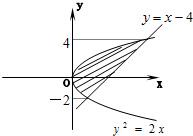
图中，阴影部分的面积是 ．
【答案】分析：从图象中知抛物线与直线的交点坐标分别为（2，-2），（8，4）．过（2，-2）作x轴的垂线把阴影部分分为S1，S2两部分，利用定积分的方法分别求出它们的面积并相加即可得到阴影部分的面积．
解答：解：从图象中知抛物线与直线的交点坐标分别为（2，-2），（8，4）．过（2，-2）作x轴的垂线把阴影部分分为S1，S2两部分，分别求出它们的面积A1，A2：
A1=∫2[
]dx=2
dx=
，
A2=∫28[
]dx=
所以阴影部分的面积A=A1+A2=
=18
故答案为18．
点评：考查学生利用定积分求阴影面积的方法的能力．
解答：解：从图象中知抛物线与直线的交点坐标分别为（2，-2），（8，4）．过（2，-2）作x轴的垂线把阴影部分分为S1，S2两部分，分别求出它们的面积A1，A2：
A1=∫2[
]dx=2dx=，A2=∫28[
]dx=所以阴影部分的面积A=A1+A2=
=18故答案为18．
点评：考查学生利用定积分求阴影面积的方法的能力．
练习册系列答案
作业辅导系列答案
相关题目
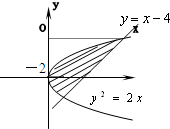图中，阴影部分的面积是（ ）| A、16 | B、18 | C、20 | D、22 |
