题目内容
 如图,正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P在棱CC1上,且∠A1PB=
如图,正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P在棱CC1上,且∠A1PB=| π | 2 |
(1)求PC的长;
(2)求钝二面角A-A1B-P的大小.
分析:(1)建立空间直角坐标系,用坐标表示点与向量,利用∠A1PB=
,可得
•
=0,由此可求PC的长;
(2)求出平面AA1B的一个法向量为
=
=(1,0,0),平面A1BP的一个法向量为
=(1,0,-1),利用向量的夹角公式,即可求得结论.
| π |
| 2 |
| A1P |
| BP |
(2)求出平面AA1B的一个法向量为
| m |
| DA |
| n |
解答: 解:(1)如图,以点D为原点O,DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系O-xyz,则D(0,0,0),B(1,1,0),A1(1,0,2),
解:(1)如图,以点D为原点O,DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系O-xyz,则D(0,0,0),B(1,1,0),A1(1,0,2),
设P(0,1,λ),其中λ∈[0,2],
因为∠A1PB=
,所以
•
=0,
即(-1,1,λ-2)•(-1,0,λ)=0,得λ=1,
此时P(0,1,1),即有PC=1;
(2)平面AA1B的一个法向量为
=
=(1,0,0),
设平面A1BP的一个法向量为
=(x,y,z),
则
即
不妨取x=1,则y=2,z=1,即
=(1,2,1),
所以cos<
,
>=
=
,
所以,钝二面角A-A1B-P的大小为π-arccos
.
 解:(1)如图,以点D为原点O,DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系O-xyz,则D(0,0,0),B(1,1,0),A1(1,0,2),
解:(1)如图,以点D为原点O,DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系O-xyz,则D(0,0,0),B(1,1,0),A1(1,0,2),设P(0,1,λ),其中λ∈[0,2],
因为∠A1PB=
| π |
| 2 |
| A1P |
| BP |
即(-1,1,λ-2)•(-1,0,λ)=0,得λ=1,
此时P(0,1,1),即有PC=1;
(2)平面AA1B的一个法向量为
| m |
| DA |
设平面A1BP的一个法向量为
| n |
则
|
|
不妨取x=1,则y=2,z=1,即
| n |
所以cos<
| m |
| n |
| 1 | ||
|
| ||
| 6 |
所以,钝二面角A-A1B-P的大小为π-arccos
| ||
| 6 |
点评:本题主要考查空间向量的应用,考查向量的夹角公式,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
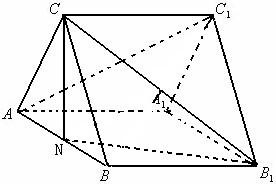 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
