题目内容
如图所示,已知正方体ABCD—A1B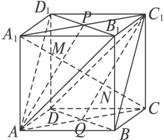
(1)求证:平面AB1D1∥平面C1BD;
(2)求平面AB1D1和平面C1BD间的距离.
(1)证明:

∵ABCD—A1B
∴B1D1∥平面C1BD.
同理,D
(2)解:如图,连结A
由于A
∴A
同理A
因此MN的长即是两个平行平面AB1D1和C1BD的距离.
在矩形A1ACC1中,∵AA1=CC1=a,AC=A![]() ,∴A
,∴A![]() .
.
设平面AB1D1和平面A1ACC1交于直线AP(其中P设为B1D1的中点),则M在直线AP上,又平面BDC1和平面A1ACC1交于C1Q(其中Q设为BD的中点),
∴N在直线C1Q上,且AP∥C1Q,由平面几何知识M、N是A
∴MN=![]() ,此即为平面AB1D1和平面C1BD间的距离.
,此即为平面AB1D1和平面C1BD间的距离.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
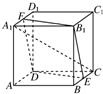 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.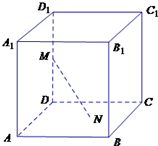 如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )
如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )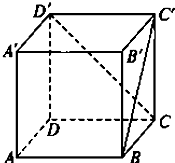 如图所示,已知正方体ABCD-A′B′C′D′,求:
如图所示,已知正方体ABCD-A′B′C′D′,求: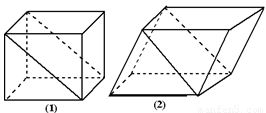
 的概率P1;
的概率P1; 的概率P2。
的概率P2。