题目内容
设f(x)是定义在R上函数,若x1、x2∈[0, ]时,f(x1+x2)=f(x1)•f(x2)且f(1)=b>0,求
]时,f(x1+x2)=f(x1)•f(x2)且f(1)=b>0,求 、
、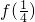 .
.
解:令x1=x2=x∈[0, ],得f(2x)=f2(x)>0
],得f(2x)=f2(x)>0
∴f(x)>0
令x1=x2= ,得f(
,得f(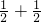 )=f(
)=f( )
) =b
=b
∴f( )=
)=
令x1=x2= ,得f(
,得f( +
+ )=f(
)=f( )f(
)f( )=
)=
∴f( )=
)=
分析:先令x1=x2=x∈[0, ],确定出f(x)的符号,再令x1=x2=
],确定出f(x)的符号,再令x1=x2= ,求出f(
,求出f( )的值,最后令x1=x2=
)的值,最后令x1=x2= ,求出f(
,求出f( )的值.
)的值.
点评:本题主要考查了抽象函数及其应用,以及赋值法的运用,属于基础题.
 ],得f(2x)=f2(x)>0
],得f(2x)=f2(x)>0∴f(x)>0
令x1=x2=
 ,得f(
,得f(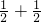 )=f(
)=f( )
) =b
=b∴f(
 )=
)=
令x1=x2=
 ,得f(
,得f( +
+ )=f(
)=f( )f(
)f( )=
)=
∴f(
 )=
)=
分析:先令x1=x2=x∈[0,
 ],确定出f(x)的符号,再令x1=x2=
],确定出f(x)的符号,再令x1=x2= ,求出f(
,求出f( )的值,最后令x1=x2=
)的值,最后令x1=x2= ,求出f(
,求出f( )的值.
)的值.点评:本题主要考查了抽象函数及其应用,以及赋值法的运用,属于基础题.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |