题目内容
如图正三棱柱
，
,
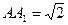，若
为棱
中点.
（Ⅰ）求证：
∥平面
；
（Ⅱ）求
与平面所成的角正弦值.
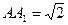，,，若为棱中点.（Ⅰ）求证：
∥平面；（Ⅱ）求
与平面所成的角正弦值.正弦值为
（Ⅰ）连结
和
交于
点，连
．
∵是正三棱柱， 
∴为的中点.又为棱中点,
∴在
中,
,又
,
平面,
∴∥平面；………………………………………6分
（Ⅱ）建如图所示空间直角坐标系，
∵
，
，
，
，
，
∴
， 
设平面的法向量为n
，
∴
，即
，令
，得n
，
∵
∴
，
∴与平面所成的角正弦值为.……………13分
和交于点，连．∵
是正三棱柱， ∴
为的中点.又为棱中点,∴在
中,,又,平面,∴
∥平面；………………………………………6分（Ⅱ）建如图所示空间直角坐标系，∵
，，，，，∴
， 设平面
的法向量为n，∴
，即，令，得n，∵
∴，∴
与平面所成的角正弦值为.……………13分
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
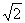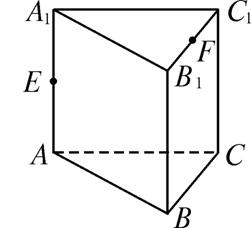
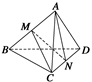
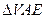,BB1=2,∠ABC=90°,E、F分为AA1、C1B1的中点，沿棱柱的表面从E到F两点的最短路径的长度是________. 
的面积是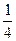
，则侧棱VA与底面所成角的大小是__________________（结果用反三角函数值表示）。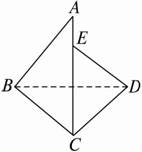
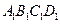的棱长为l，点F、H分别为为
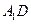、A1C的中点．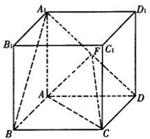
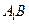∥平面AFC；．
平面AFC.