题目内容
已知定义域为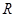 的函数
的函数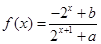 是奇函数.
是奇函数.
(1)求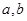 的值;
的值;
(2)判断函数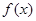 的单调性,并证明.
的单调性,并证明.
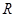 的函数
的函数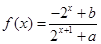 是奇函数.
是奇函数.(1)求
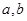 的值;
的值;(2)判断函数
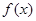 的单调性,并证明.
的单调性,并证明.(1) ;(2)减函数,证明详见解析;
;(2)减函数,证明详见解析;
 ;(2)减函数,证明详见解析;
;(2)减函数,证明详见解析;试题分析:(1)因为
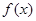 是奇函数,且定义域为
是奇函数,且定义域为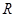 ,可由
,可由 和
和 列式求出
列式求出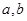 的值,但要注意
的值,但要注意 和
和 只是本题中的
只是本题中的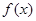 是奇函数的必要条件,然后还要验证充分性;(2)判断函数的单调性在解答题中一般利用增函数或减函数的定义,或利用导函数的符号判断.
是奇函数的必要条件,然后还要验证充分性;(2)判断函数的单调性在解答题中一般利用增函数或减函数的定义,或利用导函数的符号判断.试题解析:(1)因为
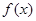 是奇函数,且定义域为
是奇函数,且定义域为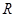 ,所以
,所以 , 2分
, 2分所以
 ,所以
,所以 4分
4分又
 ,知
,知
经验证,当
 时,
时,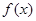 是奇函数,所以
是奇函数,所以 7分
7分(2)函数
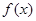 在
在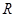 上为减函数 9分
上为减函数 9分证明:法一:由(1)知
 ,
,令
 ,则
,则 ,
, 12分
12分 ,
,即
 ,
, 函数
函数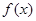 在
在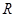 上为减函数 14分
上为减函数 14分法二:由(1)知
 ,
, , 12分
, 12分 ,
,即

 函数
函数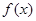 在
在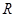 上为减函数. 14分
上为减函数. 14分
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
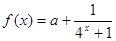 是奇函数.
是奇函数.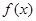 的单调性并证明;
的单调性并证明;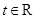 ,不等式
,不等式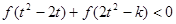 恒成立,求
恒成立,求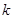 的取值范围.
的取值范围.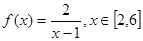 ,试判断此函数
,试判断此函数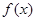 在
在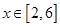 上的单调性,并求此函数
上的单调性,并求此函数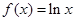 ,
,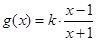 .
.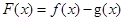 的单调区间;
的单调区间;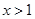 时,函数
时,函数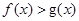 恒成立,求实数
恒成立,求实数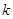 的取值范围;
的取值范围;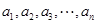 满足
满足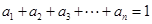 ,求证:
,求证: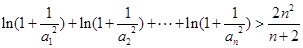 .
.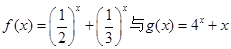 的交点的横坐标为
的交点的横坐标为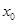 ,当
,当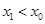 时
时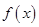
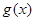 (从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)
(从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)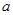 、
、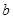 为正实数,函数
为正实数,函数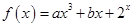 在
在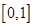 上的最大值为
上的最大值为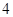 ,则
,则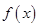 在
在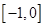 上的最小值为 .
上的最小值为 .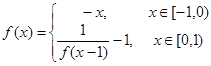 ,若方程
,若方程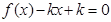 有两个实数根,则
有两个实数根,则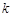 的取值范围是( )
的取值范围是( )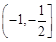
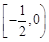
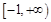
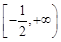
 在
在 上的最大值和最小值分别是( )
上的最大值和最小值分别是( )