题目内容
已知 ,且
,且 ,
,
(1)求cosα的值;
(2)若 ,
,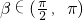 ,求cosβ的值.
,求cosβ的值.
解:(1)由 ,平方可得 sinα=
,平方可得 sinα= ,再由已知
,再由已知 ,
,
可得 α= ,∴cosα=-
,∴cosα=- .
.
(2)∵ ,
,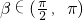 ,∴-
,∴- <α-β<
<α-β< ,cos(α-β)=
,cos(α-β)= .
.
∴cosβ=cos(-β)=cos[(α-β )-α]=cos(α-β)cosα+sin(α-β)sinα
= +
+ =-
=- .
.
分析:(1)把已知条件平方可得sinα= ,再由已知
,再由已知 ,可得cosα的值.
,可得cosα的值.
(2)由条件可得- <α-β<
<α-β< ,cos(α-β)=
,cos(α-β)= ,再根据cosβ=cos(-β)=cos[(α-β )-α],利用两角和差的
,再根据cosβ=cos(-β)=cos[(α-β )-α],利用两角和差的
余弦公式,运算求得结果.
点评:本题主要考查同角三角函数的基本关系,二倍角公式、两角和差的余弦公式的应用,属于中档题.
 ,平方可得 sinα=
,平方可得 sinα= ,再由已知
,再由已知 ,
,可得 α=
 ,∴cosα=-
,∴cosα=- .
.(2)∵
 ,
,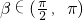 ,∴-
,∴- <α-β<
<α-β< ,cos(α-β)=
,cos(α-β)= .
.∴cosβ=cos(-β)=cos[(α-β )-α]=cos(α-β)cosα+sin(α-β)sinα
=
 +
+ =-
=- .
.分析:(1)把已知条件平方可得sinα=
 ,再由已知
,再由已知 ,可得cosα的值.
,可得cosα的值.(2)由条件可得-
 <α-β<
<α-β< ,cos(α-β)=
,cos(α-β)= ,再根据cosβ=cos(-β)=cos[(α-β )-α],利用两角和差的
,再根据cosβ=cos(-β)=cos[(α-β )-α],利用两角和差的余弦公式,运算求得结果.
点评:本题主要考查同角三角函数的基本关系,二倍角公式、两角和差的余弦公式的应用,属于中档题.

练习册系列答案
相关题目
 ,
, 且
且 .
.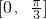 上的最大值.
上的最大值.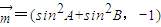 ,
,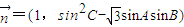 且
且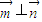 .
.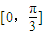 上的最大值.
上的最大值.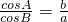 ,且
,且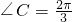 .
.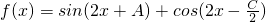 ,求函数f(x)在
,求函数f(x)在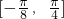 上的值域.
上的值域.