题目内容
已知函数f（x）=4sin?x+3cosωx（x∈R）满足f（m）=-5，f（n）=0，且|m-n|的最小值为π，则正数ω的值为 ．
【答案】分析：化简函数的表达式，根据f（m）=-5，f（n）=0以及|m-n|的最小值等于π，求出函数的周期，然后求出ω的值．
解答：解：函数f（x）=4sin?x+3cosωx=5sin（ωx+φ），tanφ=
，
因为f（m）=-5，f（n）=0，且|m-n|的最小值等于π，
所以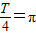
，T=4π，所以T=
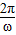=4π，
所以ω=
．
故答案为：
．
点评：本题是基础题，考查三角函数的化简，周期的求法，正确分析题意找出函数满足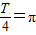
是解题的重点关键，考查逻辑推理能力，计算能力．
解答：解：函数f（x）=4sin?x+3cosωx=5sin（ωx+φ），tanφ=
，因为f（m）=-5，f（n）=0，且|m-n|的最小值等于π，
所以
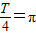，T=4π，所以T=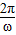=4π，所以ω=
．故答案为：
．点评：本题是基础题，考查三角函数的化简，周期的求法，正确分析题意找出函数满足
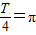是解题的重点关键，考查逻辑推理能力，计算能力． 
练习册系列答案
浙江名校名师金卷系列答案
相关题目