题目内容
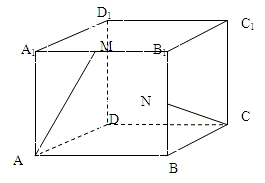在正方体ABCD-A1B1C1D1中，棱长为a，M为A1B1的中点，N为BB1的中点．
（1）求异面直线AM与CN所成角的大小；
（2）求四面体N-AMC的体积．
解：（1）以D为坐标原点，以DA，DC，DD1分别为x轴y轴z轴建立空间直角坐标系
则 A（a，0，0）C（0，a，0）
∴
，
设
夹角为θ，
=
∴
∴异面直线AM与CN所成角为
（2）
而
=
∴
分析：（1）利用空间向量求异面直线所成角，就是把异面直线所成角转化为空间向量的夹角，本题中，建立空间直角坐标系，异面直线AM与CN所成角即的夹角，再用向量的夹角公式计算即可．
（2）欲求四面体N-AMC的体积，只需用割补法，把四面体N-AMC看做以△AMN为底面，以CB为高，利用三棱锥的体积公式计算即可．
点评：本题主要考查了利用空间向量求异面直线所成角，以及三棱锥体积公式的应用．
则 A（a，0，0）C（0，a，0）
∴
，设
夹角为θ，=∴∴异面直线AM与CN所成角为
（2）
而
=∴
分析：（1）利用空间向量求异面直线所成角，就是把异面直线所成角转化为空间向量的夹角，本题中，建立空间直角坐标系，异面直线AM与CN所成角即
的夹角，再用向量的夹角公式计算即可．（2）欲求四面体N-AMC的体积，只需用割补法，把四面体N-AMC看做以△AMN为底面，以CB为高，利用三棱锥的体积公式计算即可．
点评：本题主要考查了利用空间向量求异面直线所成角，以及三棱锥体积公式的应用．
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）