题目内容
椭圆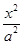 +
+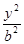 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是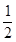 ,则
,则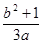 的最小值为( )
的最小值为( )
A.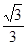 | B.1 | C.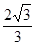 | D.2 |
A
解析试题分析:因为椭圆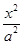 +
+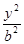 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是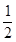 ,所以
,所以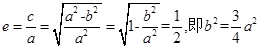 ,
,
所以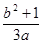
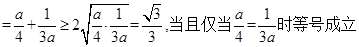 ,所以
,所以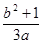 的最小值为
的最小值为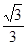 。
。
考点:椭圆的简单性质;基本不等式。
点评:直接考查椭圆的离心率和基本不等式的综合应用。注意基本不等式应用的条件:一正二定三相等。

练习册系列答案
相关题目
过抛物线y2=2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P,Q两点,分别作PP¢、QQ¢垂直于抛物线的准线于P¢、Q¢,若|PQ|=2,则四边形PP¢Q¢Q的面积为
| A.1 | B.2 | C. | D.3 |
已知双曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,则满足△
,则满足△ 的周长为
的周长为 的动点
的动点 的轨迹方程为 ( )
的轨迹方程为 ( )
A. | B. | C. | D. |
如果方程 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则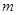 的取值范围是
的取值范围是
A. | B. | C. | D. |
与椭圆 共焦点且过点(5,-2)的双曲线标准方程是
共焦点且过点(5,-2)的双曲线标准方程是
A. | B. | C. | D. |
设 ,则双曲线
,则双曲线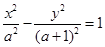 的离心率
的离心率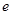 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
抛物线 的焦点坐标与准线方程( )
的焦点坐标与准线方程( )
A.焦点: ,准线: ,准线: | B.焦点: ,准线: ,准线: |
C.焦点: , 准线: , 准线: | D.焦点: , 准线: , 准线: |
 的焦点
的焦点 恰好是曲线
恰好是曲线 的右焦点,且曲线
的右焦点,且曲线 与曲线
与曲线 交点连线过点
交点连线过点



 ,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且
,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )
 B、
B、 C、
C、 D、
D、