题目内容
已知单位向量e1与e2的夹角为60°,且a=2e1+e2,b=-3e1+2e2,求a·b及a与b的夹角α.
解析:∵e1、e2是夹角为60°的单位向量,
∴e1·e2=|e1||e2|cos60°=![]() .
.
∴a·b=(2e1+e2)·(-3e1+2e2)
=-6e12+e1·e2+2e22
=-6|e1|2+e1·e2+2|e2|2
=-![]()
又∵|a|2=|2e1+e2|2=(2e1+e2)2=4e12+4e1·e2+e22=7,
|b|2=b2=(-3e1+2e2)2=9e12-12e1·e2+4e22=7,
∴|a|=![]() ,|b|=
,|b|=![]() .
.
∴cosα=![]() =
=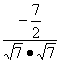 =-
=-![]() .
.
∴α=120°.
综上所述,a·b=-![]() ,α=120°.
,α=120°.
点评:由于e1与e2夹角为60°,模为1,故可求e1·e2以及e12、e22,再利用模的公式,可以求出|a|与|b|,然后逆用数量积公式,解出夹角α.

练习册系列答案
相关题目
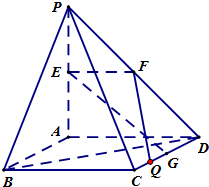 (理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.